
| A. | 7和8 | B. | 6和7 | C. | 5和6 | D. | 4和5 |
分析 根据题意,求出首项a1与公差d的关系,得出通项公式an,利用Sn+1≤Sn,得出$\left\{\begin{array}{l}{{a}_{n}≥0}\\{{a}_{n+1}≤0}\end{array}\right.$,由此求出n的值.
解答 解:等差数列中,∵|a3|=|a9|,
∴a32=a92,
即(a1+2d)2=(a1+8d)2,
∴a1=-5d,
∴an=a1+(n-1)d=(n-6)d;
又Sn+1≤Sn,
∴$\left\{\begin{array}{l}{{a}_{n}≥0}\\{{a}_{n+1}≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{(n-6)d≥0}\\{(n+1-6)d≤0}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{n-6≤0}\\{n-5≥0}\end{array}\right.$,
解得5≤n≤6.
故选:C.
点评 本题考查了等差数列的前n项和以及灵活运用等差数列的通项公式解决问题的能力,是中档题目.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 8或9 | D. | 9或10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
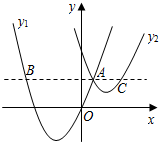 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com