
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() 恒成立,证明:当
恒成立,证明:当![]() 时,
时,![]() .
.
【答案】(1)详见解析;(2)详见解析
【解析】
试题分析:熟练掌握利用导数研究函数的单调性、极值、等价转化、分类讨论的思想方法等是解题的关键.(I)利用导数的运算法则可得![]() ,对
,对![]() 分类讨论即可得出其单调性;(II)通过对
分类讨论即可得出其单调性;(II)通过对![]() 分类讨论,得到当
分类讨论,得到当![]() ,满足条件且
,满足条件且![]() (当且仅当x=1时取“=”).利用此结论即可证明.
(当且仅当x=1时取“=”).利用此结论即可证明.
试题解析: 解:(Ⅰ)求导得![]()
若a≤0,f′(x)>0,f(x)在(0,+∞)上递增;
若a>0,当x∈(0,![]()
![]() )时,f′(x)>0,f(x)单调递增;
)时,f′(x)>0,f(x)单调递增;
当x∈(![]()
![]() ,+∞)时,f′(x)<0,f(x)单调递减.
,+∞)时,f′(x)<0,f(x)单调递减.
(Ⅱ)由(Ⅰ)知,
若a≤0,f(x)在(0,+∞)上递增,又f(1)=0,故f(x)≤0不恒成立
若a>2,当x∈(![]() ,1)时,f(x)递减,f(x)>f(1)=0,不合题意
,1)时,f(x)递减,f(x)>f(1)=0,不合题意
若0<a<2,当x∈(1,![]()
![]() )时,f(x)递增,f(x)>f(1)=0,不合题意
)时,f(x)递增,f(x)>f(1)=0,不合题意
若a=2,f(x)在(0,1)上递增,在(1,+∞)上递减,
f(x)≤f(1)=0,合题意
故a=2,且lnx≤x﹣1(当且仅当x=1时取“=”).
当0<x1<x2时,f(x2)﹣f(x1)=2ln![]() ﹣2(x2﹣x1)
﹣2(x2﹣x1)
<2(![]() ﹣1)﹣2(x2﹣x1)=2(
﹣1)﹣2(x2﹣x1)=2(![]() ﹣1)(x2﹣x1),
﹣1)(x2﹣x1),
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,△
为矩形,△![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.

(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年
的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年![]() 位居民毎人的月均用水量(单位:吨),将数据按照
位居民毎人的月均用水量(单位:吨),将数据按照![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.
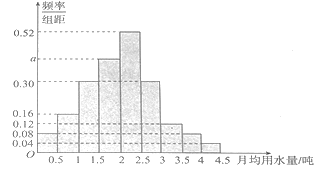
(1)求直方图中![]() 的值;
的值;
(2)若该市有![]() 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于![]() 吨的人数,并说明理由;
吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到
的值(精确到![]() ),并说明理由.
),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
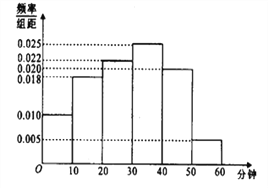
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(参考公式![]() ,其中
,其中![]() .)
.)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上横坐标为
,抛物线上横坐标为![]() 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是块矩形硬纸板,其中AB=2AD,AD=![]() ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
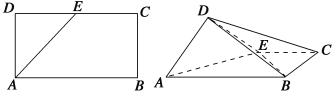
(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com