
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:不详 题型:单选题
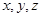 ,定义运算
,定义运算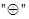 满足:(1)
满足:(1)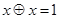 ; (2)
; (2)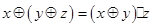 .若
.若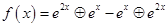 ,则下列判断正确的是( )
,则下列判断正确的是( )A.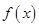 是增函数又是奇函数 是增函数又是奇函数 | B.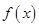 是减函数又是奇函数 是减函数又是奇函数 |
C.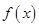 是增函数又是偶函数 是增函数又是偶函数 | D.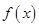 是减函数又是偶函数 是减函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
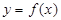 的定义域为
的定义域为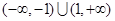 ,其图象上任一点
,其图象上任一点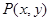 满足
满足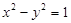 ,则给出以下四个命题:
,则给出以下四个命题: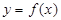 一定是偶函数; ②函数
一定是偶函数; ②函数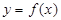 可能是奇函数;
可能是奇函数;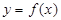 在
在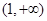 单调递增; ④若
单调递增; ④若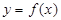 是偶函数,其值域为
是偶函数,其值域为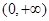
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 中定义一种运算“
中定义一种运算“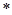 ”,对任意
”,对任意 ,
, 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质: ,
, ;
;  ,
, .
. 的性质,有如下说法:①函数
的性质,有如下说法:①函数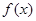 的最小值为
的最小值为 ;②函数
;②函数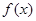 为偶函数;③函数
为偶函数;③函数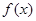 的单调递增区间为
的单调递增区间为 .
.A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com