
،¾جâؤ؟،؟ؤ³×¨آôµêدْتغز»ذآ؟î·×°£¬بصدْتغء؟£¨µ¥خ»خھ¼£©f(n) سëت±¼نn£¨1،ـn،ـ30،¢n![]() N*£©µؤ؛¯ت¹طدµبçدآح¼ثùت¾£¬ئنضذ؛¯تf(n) ح¼دَضذµؤµمخ»سعذ±آتخھ 5 ؛ح£3 µؤء½جُض±دكةد£¬ء½ض±دك½»µمµؤ؛ل×ّ±êخھm£¬ازµعmجىبصدْتغء؟×î´َ.
N*£©µؤ؛¯ت¹طدµبçدآح¼ثùت¾£¬ئنضذ؛¯تf(n) ح¼دَضذµؤµمخ»سعذ±آتخھ 5 ؛ح£3 µؤء½جُض±دكةد£¬ء½ض±دك½»µمµؤ؛ل×ّ±êخھm£¬ازµعmجىبصدْتغء؟×î´َ.
(¢ٌ)اَf(n) µؤ±ي´ïت½£¬¼°ا°mجىµؤدْتغ×ـت£»
(¢ٍ)°´زشحù¾ر飬µ±¸أרآôµêدْتغؤ³؟î·×°µؤ×ـت³¬¹ 400 ¼ت±£¬تذأوةد»لء÷ذذ¸أ؟î·×°£¬¶ّبصدْتغء؟ء¬ذّدآ½µ²¢µحسع 30 ¼ت±£¬¸أ؟î·×°½«²»شظء÷ذذ.تشش¤²â±¾؟î·×°شعتذأوةدء÷ذذµؤجىتتا·ٌ»ل³¬¹ 10 جى£؟اëثµأ÷ہيسة.
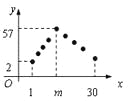
،¾´ً°¸،؟(¢ٌ)  £¬£¨n
£¬£¨n![]() N*£©£¬354 ¼£»(¢ٍ) ²»³¬¹£¬ہيسة¼û½âخِ.
N*£©£¬354 ¼£»(¢ٍ) ²»³¬¹£¬ہيسة¼û½âخِ.
،¾½âخِ،؟
(I) ¸ù¾فجâز⣬ةè £¬
£¬
¶ّf(1) = 2£¬،à 5 +a= 2,a= £3£®
سض 5m+a= £3m+b£¬،àb= 8m+a= 8m£3£¬
،à £®
£®
سةf(m) = 57µأm= 12£®
![]()
ا° 12 جىµؤدْتغ×ـء؟خھ 5 (1 + 2 + 3 + ، + 12)£3،ء12 = 354¼£®
(II) µع 13 جىµؤدْتغء؟خھf(13) = £3،ء13 + 93 =" 54" ¼£¬
¶ّ 354 + 54 > 400 ¼£¬
،à ´سµع 14 جى؟ھت¼دْتغ×ـء؟³¬¹ 400 ¼£¬¼´؟ھت¼ء÷ذذ£®
ةèµعx جىµؤبصدْتغء؟؟ھت¼µحسع 30 ¼ (12 <x،ـ 30)£¬
¼´f(x) = £3x+ 93 < 30 £¬
½âµأx> 21£®
´سµع22جى£¬بصدْتغء؟؟ھت¼µحسع 30 ¼£¬21-13=8£¬
،à¸أ·×°ء÷ذذµؤت±¼ن²»³¬¹10جى£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ؛¯ت![]() شعµم
شعµم![]() ´¦اذدكµؤذ±آتخھ1.
´¦اذدكµؤذ±آتخھ1.
£¨1£©اَ![]() µؤضµ£»
µؤضµ£»
£¨2£©ةè![]() £¬بô¶شبخزâ
£¬بô¶شبخزâ![]() £¬¶¼سذ
£¬¶¼سذ![]() £¬اَتµت
£¬اَتµت![]() µؤب،ضµ·¶خ§.
µؤب،ضµ·¶خ§.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟دض¶شؤ³تذ¹¤ذ½½×²م¹طسع،°آ¥تذدق¹؛ءî،±µؤج¬¶ب½ّذذµ÷²é,ثو»ْ³éµ÷ءث50بث,ثûأاشآتصبëµؤئµت·ض²¼¼°¶ش،°آ¥تذدق¹؛ءî،±شق³ةبثتبç±ي:
شآتصبë(µ¥خ»°ظشھ) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
ئµت | 5 | 10 | 15 | 10 | 5 | 5 |
شق³ةبثت | 4 | 8 | 12 | 5 | 2 | 1 |
(¢ٌ)سةزشةدح³¼ئت¾فجîدآأو2،ء2ءذءھ±ي²¢ختتا·ٌسذ99%µؤ°رخصبدخھ،°شآتصبëزش5500خھ·ض½çµم،±¶ش،°آ¥تذدق¹؛ءî،±µؤج¬¶بسذ²îزى;
شآتصبëµحسع55°ظشھµؤبثت | شآتصبë²»µحسع55°ظشھµؤبثت | ؛د¼ئ | |
شق³ة | |||
²»شق³ة | |||
؛د¼ئ |
(¢ٍ)بô²ةسأ·ض²م³éرùشعشآتصبëشع[15,25),[25,35)µؤ±»µ÷²éبثضذ¹²ثو»ْ³éب،6بث½ّذذ×·×ظµ÷²é,²¢¸ّسèئنضذ3بث،°؛ى°ü،±½±ہّ,اَتصµ½،°؛ى°ü،±½±ہّµؤ3بثضذضءةظسذ1بثتصبëشع[15,25)µؤ¸إآت.
²خ؟¼¹«ت½:K2![]() ,ئنضذn=a+b+c+d.
,ئنضذn=a+b+c+d.
²خ؟¼ت¾ف:
P(K2،فk) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھµم![]() £®بôاْدك
£®بôاْدك![]() ةد´وشع
ةد´وشع![]() £¬
£¬![]() ء½µم£¬ت¹
ء½µم£¬ت¹![]() خھصب½اذخ£¬شٍ³ئ
خھصب½اذخ£¬شٍ³ئ![]() خھ
خھ![]() ذحاْدك£®¸ّ¶¨دآءذبجُاْدك£؛
ذحاْدك£®¸ّ¶¨دآءذبجُاْدك£؛
¢ظ![]() £»
£»
¢ع![]() £»
£»
¢غ![]() £®
£®
ئنضذ![]() ذحاْدكµؤ¸ِتتا
ذحاْدكµؤ¸ِتتا
A.![]() B.
B.![]()
C.![]() D.
D.![]()
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ؛¯ت![]() .
.
£¨1£©بôاْدك![]() شع
شع![]() ´¦µؤاذدكµؤذ±آتخھ2£¬اَ؛¯ت
´¦µؤاذدكµؤذ±آتخھ2£¬اَ؛¯ت![]() µؤµ¥µ÷اّ¼ن£»
µؤµ¥µ÷اّ¼ن£»
£¨2£©بô؛¯ت![]() شعاّ¼ن
شعاّ¼ن![]() ةدسذءمµم£¬اَتµت
ةدسذءمµم£¬اَتµت![]() µؤب،ضµ·¶خ§.£¨
µؤب،ضµ·¶خ§.£¨![]() تا×شب»¶شتµؤµ×ت£¬
تا×شب»¶شتµؤµ×ت£¬![]() £©
£©
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعبہâ׶P-ABCضذ£¬ئ½أوPAC،حئ½أوABC£¬![]() ؛ح
؛ح![]() ¶¼تاصب½اذخ£¬
¶¼تاصب½اذخ£¬![]() £¬ E،¢F·ض±ًتاAC،¢BCµؤضذµم£¬ازPD،حABسعD.
£¬ E،¢F·ض±ًتاAC،¢BCµؤضذµم£¬ازPD،حABسعD.
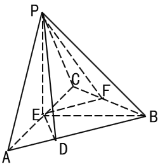
£¨¢ٌ£©ض¤أ÷£؛ض±دك![]() ،حئ½أو
،حئ½أو![]() £»
£»
£¨¢ٍ£©اَ¶أو½ا![]() µؤصدزضµ£®
µؤصدزضµ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعبہâ׶P-ABCضذ£¬ئ½أوPAC،حئ½أوABC£¬![]() ؛ح
؛ح![]() ¶¼تاصب½اذخ£¬
¶¼تاصب½اذخ£¬![]() £¬ E،¢F·ض±ًتاAC،¢BCµؤضذµم£¬ازPD،حABسعD.
£¬ E،¢F·ض±ًتاAC،¢BCµؤضذµم£¬ازPD،حABسعD.

£¨¢ٌ£©ض¤أ÷£؛ض±دك![]() ،حئ½أو
،حئ½أو![]() £»
£»
£¨¢ٍ£©اَ¶أو½ا![]() µؤصدزضµ£®
µؤصدزضµ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھتءذ![]() µؤح¨دت½خھ
µؤح¨دت½خھ![]() £¬ئنضذ
£¬ئنضذ![]() £¬
£¬![]() ،¢
،¢![]() .
.
(1)تشذ´³ِز»×é![]() ،¢
،¢![]() µؤضµ£¬ت¹µأتءذ
µؤضµ£¬ت¹µأتءذ![]() ضذµؤ¸÷دî¾ùخھصت.
ضذµؤ¸÷دî¾ùخھصت.
(2)بô![]() £¬
£¬![]() £¬تءذ
£¬تءذ![]() آْ×م
آْ×م![]() £¬از¶شبخزâµؤ
£¬از¶شبخزâµؤ![]() (
(![]() )£¬¾ùسذ
)£¬¾ùسذ![]() £¬ذ´³ِثùسذآْ×مجُ¼µؤ
£¬ذ´³ِثùسذآْ×مجُ¼µؤ![]() µؤضµ.
µؤضµ.
(3)بô![]() £¬تءذ
£¬تءذ![]() آْ×م
آْ×م![]() £¬ئنا°
£¬ئنا°![]() دî؛حخھ
دî؛حخھ![]() £¬ازت¹
£¬ازت¹![]() (
(![]() ،¢
،¢![]() £¬
£¬![]() )µؤ
)µؤ![]() ؛ح
؛ح![]() سذاز½ِسذ
سذاز½ِسذ![]() ×飬
×飬![]() ،¢
،¢![]() ،¢،،¢
،¢،،¢![]() ضذسذضءةظ
ضذسذضءةظ![]() ¸ِء¬ذّدîµؤضµدàµب£¬ئنثüدîµؤضµ¾ù²»دàµب£¬اَ
¸ِء¬ذّدîµؤضµدàµب£¬ئنثüدîµؤضµ¾ù²»دàµب£¬اَ![]() ،¢
،¢![]() µؤ×îذ،ضµ.
µؤ×îذ،ضµ.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬بہâضùABC©پA1B1C1µؤ²àأوAA1B1Bتاءâذخ£¬²àأوAA1C1Cتا¾طذخ£¬ئ½أوAA1C1C،حئ½أوAA1B1B£¬،دBAA1![]() £¬AA1=2AC=2£¬OخھAA1µؤضذµم.
£¬AA1=2AC=2£¬OخھAA1µؤضذµم.
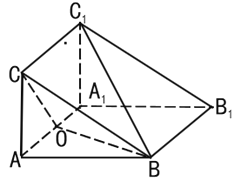
£¨1£©اَض¤:OC،حBC1£»
£¨2£©اَµمC1µ½ئ½أوABCµؤ¾àہë.
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com