
【题目】设椭圆![]() ,其长轴长是短轴长的
,其长轴长是短轴长的![]() 倍,过焦点且垂直于
倍,过焦点且垂直于![]() 轴的直线被椭圆截得的弦长为
轴的直线被椭圆截得的弦长为![]() .
.
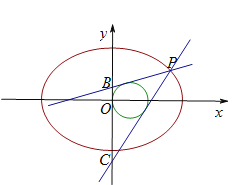
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 是椭圆
是椭圆![]() 上横坐标大于
上横坐标大于![]() 的动点,点
的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]() ,试判断点
,试判断点![]() 在何位置时
在何位置时![]() 的长度最小,并证明你的判断.
的长度最小,并证明你的判断.
【答案】(1)![]() ;(2)点
;(2)点![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度最小.见解析.
的长度最小.见解析.
【解析】
(1)根据条件列方程组,解得![]() ;
;
(2)先设![]() ,
,![]() ,根据点斜式得直线
,根据点斜式得直线![]() 的方程,再根据直线与圆相切列等量关系得
的方程,再根据直线与圆相切列等量关系得![]() ,类似可得
,类似可得![]() ,转化为
,转化为![]() 是方程
是方程![]() 的两个根,利用韦达定理解得
的两个根,利用韦达定理解得![]() ,根据
,根据![]() 点满足椭圆方程,代入化简得
点满足椭圆方程,代入化简得![]() ,最后根据
,最后根据![]() 范围以及函数单调性求最值,即得结果.
范围以及函数单调性求最值,即得结果.
(1)由已知![]() ,
,
因为过焦点且垂直于![]() 轴的直线被椭圆截得的弦长为
轴的直线被椭圆截得的弦长为![]() ,
,![]() ,
,
解得![]() ,故所求椭圆方程为
,故所求椭圆方程为![]() .
.
(2)设![]() ,
,![]() .
.
不妨设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
又圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即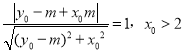 ,
,
化简得![]() 同理,
同理,![]() ,
,
![]() 是方程
是方程![]() 的两个根,
的两个根,
![]() ,则
,则![]() ,
,
![]() 是椭圆上的点,∴
是椭圆上的点,∴![]() ,
,![]() .
.
令![]() ,令
,令![]() ,则
,则![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 取到最小值,此时
取到最小值,此时![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度最小.
的长度最小.


科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,![]() 为非零常数,
为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②平面内到两定点距离之和等于常数的点的轨迹是椭圆
③若方程![]() 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则![]()
④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为________________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农业银行开始为全国农行ATM机安装刷脸取款系统.某农行营业点为调查居民对刷脸取款知识的了解情况,制作了刷脸取款知识有奖调查问卷,发放给2018年度该行的所有客户,并从参与调查且年龄(单位:岁)在[25,55]内的客户中随机抽取100名给予物质奖励,再从中选出一名客户参加幸运大抽奖.调查结果按年龄分成6组,制作成如下的频数分布表和女客户的年龄茎叶图,其中a∶b∶c=2∶4∶5.
年龄/岁 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55] |
频数/人 | 5 | a | b | c | 15 | 25 |
女客户的年龄茎叶图

幸运大抽奖方案如下:客户最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.
(1)求a,b,c的值,若分别从男、女客户中随机选取1人,求这2人的年龄均在[40,45)内的概率;
(2)若参加幸运大抽奖的客户所获奖金(单位:元)用X表示,求X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .直线
.直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .记点
.记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)已知直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与线段
处的切线与线段![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com