
【题目】如图,在四棱锥![]() 中,
中, ![]() 分别是
分别是![]() 的中点,底面
的中点,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() ,且平面
,且平面![]() 平面
平面![]() .
.
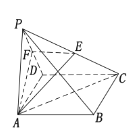
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:
【题目】数列![]() 为递增的等比数列,
为递增的等比数列, ![]()
![]() ,
,
数列![]() 满足
满足![]() .
.
(Ⅰ)求数列![]() 的通项公式;(Ⅱ)求证:
的通项公式;(Ⅱ)求证: ![]() 是等差数列;
是等差数列;
(Ⅲ)设数列![]() 满足
满足![]() ,且数列
,且数列![]() 的前
的前![]() 项和
项和![]() ,并求使得
,并求使得![]() 对任意
对任意![]() 都成立的正整数
都成立的正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据绘制茎叶图,从茎叶图看,哪种药的疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
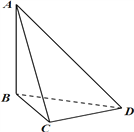
【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,则三棱锥
,则三棱锥![]() 的外接球的球面面积为__________.
的外接球的球面面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则(ⅰ)
,则(ⅰ)![]() ____________.
____________.
(ⅱ)给出下列三个命题:①函数![]() 是偶函数;②存在
是偶函数;②存在![]() ,使得以点
,使得以点![]() 为顶点的三角形是等腰三角形;③存在
为顶点的三角形是等腰三角形;③存在![]() ,使得以点
,使得以点![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.
其中,所有真命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,过右焦点且垂直于
,过右焦点且垂直于![]() 轴的直线截椭圆所得弦长是1.
轴的直线截椭圆所得弦长是1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 分别是椭圆
分别是椭圆![]() 的左,右顶点,过点
的左,右顶点,过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点(
两点(![]() 与
与![]() 不重合),证明:直线
不重合),证明:直线![]() 和直线
和直线![]() 交点的横坐标为定值.
交点的横坐标为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,即
,即![]() ,若
,若![]() ,则称
,则称![]() 在
在![]() 上封闭.
上封闭.
(1)分别判断函数![]() ,
, ![]() 在
在![]() 上是否封闭,说明理由;
上是否封闭,说明理由;
(2)函数![]() 的定义域为
的定义域为![]() ,且存在反函数
,且存在反函数![]() ,若函数
,若函数![]() 在
在![]() 上封闭,且函数
上封闭,且函数![]() 在
在![]() 上也封闭,求实数
上也封闭,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 的定义域为
的定义域为![]() ,对任意
,对任意![]() ,若
,若![]() ,有
,有![]() 恒成立,则称
恒成立,则称![]() 在
在![]() 上是单射,已知函数
上是单射,已知函数![]() 在
在![]() 上封闭且单射,并且满足
上封闭且单射,并且满足![]()
![]() ,其中
,其中![]() (
(![]() ),
),![]() ,证明:存在
,证明:存在![]() 的真子集,
的真子集, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 在所有
在所有![]() (
(![]() )上封闭.
)上封闭.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com