
����Ŀ���ס�����λͬѧ����Ϸ�����ڸ�����ʵ��a1 �� �����з�������һ�β���һ���µ�ʵ�����ɼס���ͬʱ����һö���ȵ�Ӳ�ң���������������泯�ϻ��������泯�ϣ����a1����2���ټ�ȥ12���������һ�����泯�ϣ�һ�����泯�ϣ����a1����2���ټ���12�������Ϳ��Եõ�һ���µ�ʵ��a2 �� ��ʵ��a2��������������һ�β������ֵõ�һ���µ�ʵ��a3 �� ��a3��a1 �� ��ʤ�������һ�ʤ������ʤ�ĸ���Ϊ ![]() ����a1��ȡֵ��Χ�ǣ� ��
����a1��ȡֵ��Χ�ǣ� ��
A.�����ޣ�12]
B.[24��+�ޣ�
C.��12��24��
D.�����ޣ�12]��[24��+�ޣ�
���𰸡�D
���������⣺a3�Ľ�������֣�ÿһ��������ֵĸ��ʶ��� ![]() ��
��
��a1��2a1��12��2��2a1��12����12=4a1��36=a3 ��
��a1��2a1��12�� ![]() +12=a1+6=a3 ��
+12=a1+6=a3 ��
��a1�� ![]() +12����
+12���� ![]() +12��/2+12=
+12��/2+12= ![]() +18=a3 ��
+18=a3 ��
��a1�� ![]() +12��2��
+12��2�� ![]() +12����12=a1+12=a3 ��
+12����12=a1+12=a3 ��
��a1+18��a1 �� a1+36��a1 ��
��Ҫʹ��ʤ�ĸ���Ϊ ![]() ��
��
��a3��a1�ĸ���Ϊ ![]() ��
��
��4a1��36��a1 �� ![]() +18��a1 ��
+18��a1 ��
��4a1��36��a1 �� ![]() +18��a1 ��
+18��a1 ��
���a1��12��a1��24��
��ѡD��


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={a2 �� a+1����3}��B={a��3��a2+1��2a��1}��A��B={��3}����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD��A1B1C1D1Ϊ�����壬������۴�����ǣ� �� 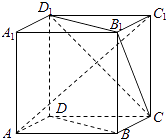
A.BD��ƽ��CB1D1
B.AC1��BD
C.����ֱ��AD��CB1��Ϊ60��
D.AC1��ƽ��CB1D1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������ռ�ֱ������ϵDxyz����֪������ABCD��A1B1C1D1���ⳤΪ1����M��������Խ���D1B���е㣬��N����CC1�ϣ� 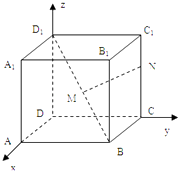
��1����2|C1N|=|NC|ʱ����|MN|��
��2������N����CC1���ƶ�ʱ����|MN|����Сֵ�����ʱ��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD��A1B1C1D1�У�����ABCDΪ�������Σ�AB��CD��AB=4��BC=CD=2��AA1=2��M��N�ֱ�����AA1��AD���е㣬��E����AB���е㣮 
��1����֤��MN��ƽ��CEC1��
��2����ƽ��D1EC1��ƽ��ABCD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����Բ
����Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
�� ![]() Ϊ��Բ�ϵ�����һ�㣬��
Ϊ��Բ�ϵ�����һ�㣬��![]() �ɵȲ�����.
�ɵȲ�����.
��1������Բ![]() �ı����̣�
�ı����̣�
��2��ֱ��![]() ����Բ��
����Բ��![]() ���㣬����
���㣬����![]() ʼ������
ʼ������![]() Ϊֱ����Բ�⣬��ʵ��
Ϊֱ����Բ�⣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��bΪ����ֱ�ߣ�������Ϊ����ƽ�棬�����ĸ������У���ȷ�������ǣ� ��
A.��a��b������ɵĽ���ȣ������b
B.��a����b�֣����֣���a��b
C.��a����b�£�����b������Φ�
D.��a�ͦ���b�ͦ£����ͦ£���a��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������㣺 ![]() ��������23=3�������е�ʽ���ܳ������ǣ� ��
��������23=3�������е�ʽ���ܳ������ǣ� ��
A.ab=ba
B.��ab��c=a��bc��
C.��ab��2=a2b2
D.c��ab��=��ca����cb����c��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1������![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ���������ȷ��ʵ��
���������ȷ��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��֤��![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com