
分析 (1)运用向量共线和垂直的条件,解方程可得x,y,即可得到所求向量;
(2)求得2$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{c}$的坐标,运用向量的模的公式和向量数量积的坐标表示,计算即可得到所求值.
解答 解(1)因为向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(9,x),$\overrightarrow{c}$=(4,y),且$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{a}$⊥$\overrightarrow{c}$.
所以3x=4×9,12+4y=0,
解得x=12,y=-3,
所以$\overrightarrow{b}$=(9,12),$\overrightarrow{c}$=(4,-3),
(2)2$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,-4),$\overrightarrow{a}$+$\overrightarrow{c}$=(7,1),
则cosθ=$\frac{(2\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}+\overrightarrow{c})}{|2\overrightarrow{a}-\overrightarrow{b}|•|\overrightarrow{a}+\overrightarrow{c}|}$=$\frac{-3×7-4}{\sqrt{9+16}•\sqrt{49+1}}$=-$\frac{\sqrt{2}}{2}$.
点评 本题考查平面向量共线和向量垂直的条件,以及向量夹角公式的运用,考查方程思想和运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±4x | C. | $y=±\frac{1}{4}x$ | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$i | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{e^3},\frac{1}{e^2})$ | B. | $(\frac{1}{e^2},\frac{1}{e})$ | C. | $(\frac{1}{e},\frac{1}{{\sqrt{e}}})$ | D. | $(\frac{1}{{\sqrt{e}}},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | [-2,2] | C. | (-∞,-4)∪(4,+∞) | D. | [-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
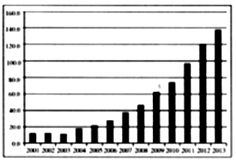 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=aax+b | D. | y=alnx+b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com