
【题目】某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.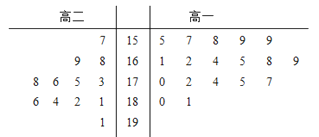
(1)如果从所有运动员中用分层抽样抽取“合格”与“不合格”的人数共10人,问就抽取“合格”人数是多少?
(2)若从所有“合格”运动员中选取2名,用X表示所选运动员来自高一队的人数,试写出X的分布图,并求X的数学期望.
【答案】解:(1)根据茎叶图可得:“合格”的人数有12,“不合格”人数有18,
用分层抽样的方法,每个运动员被抽中的概率是![]() =
=![]() ,
,
所以抽取“合格”人数是12×![]() =4
=4
(2)以题意得:X的值为:0,1,2.
则P(X=0)=![]() =
=![]() =
=![]() ,
,
P(X=1)=![]() =
=![]() =
=![]() ,
,
P(X=2)=![]() =
=![]() =
=![]()
X的分布:
X | 0 | 1 | 2 |
P |
|
|
|
X的数学期望:0×![]() +1x
+1x![]() +2x
+2x![]() =
=![]() =
=![]()
【解析】(1)运用分层抽样求解.
(2)先确定X的值为:0,1,2.再求P(X=0),P(X=1),P(X=2)
列出概率分布,求出数学期望.
【考点精析】根据题目的已知条件,利用茎叶图的相关知识可以得到问题的答案,需要掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(x)=f(2-x),且对任意的x1,x2∈(-∞,1](x1≠x2)有(x1-x2)(f(x1)-f(x2))<0.则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①圆![]() 与直线
与直线![]() 相交,所得弦长为
相交,所得弦长为![]() ;
;
②直线![]() 与圆
与圆![]() 恒有公共点;
恒有公共点;
③若棱长为![]() 的正方体的顶点都在同一球面上,则该球的表面积为
的正方体的顶点都在同一球面上,则该球的表面积为![]() ;
;
④若棱长为![]() 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为![]() .
.
其中,正确命题的序号为__________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}共有5项,其中a1=0,a5=2,且|ai+1﹣ai|=1,i=1,2,3,4,则满足条件的不同数列的个数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x),满足f(2)=0,函数y=f(x+1)的图象关于点(-1,0)中心对称,且对任意的负数x1,x2(x1≠x2),![]() 恒成立,则不等式f(x)<0的解集为____.
恒成立,则不等式f(x)<0的解集为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中a∈R).
(其中a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由.
(2)若![]() ,试判断函数f(x)在区间[1,+∞)上的单调性,并用函数单调性定义给出证明.
,试判断函数f(x)在区间[1,+∞)上的单调性,并用函数单调性定义给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足:对于任意的实数x,y都有f(x+y)=f(x)+f(y)成立,且当x<0时,f(x)>0恒成立,且nf(x)=f(nx).(n是一个给定的正整数).
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)证明f(x)为减函数;若函数f(x)在[-2,5]上总有f(x)≤10成立,试确定f(1)应满足的条件;
(3)当a<0时,解关于x的不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com