
【题目】已知函数![]() ;
;
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且当
,且当![]() ,
,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式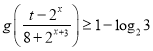 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据对数函数的真数部分大于0,及对数的运算性质,可将不等式化为![]() ,且
,且![]() 且
且![]() ,解不等式组可得
,解不等式组可得![]() 的取值范围;
的取值范围;
(2)利用奇偶性得出![]() ,
,![]() ,转化得出当
,转化得出当![]() 时,
时,![]() ,当
,当![]() 时,根据函数的奇偶性求解即可.
时,根据函数的奇偶性求解即可.
(3)关于![]() 的不等式关于
的不等式关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立,即
上恒成立,即![]()
![]() ,分类讨论后,综合讨论结果,可得实数
,分类讨论后,综合讨论结果,可得实数![]() 的取值范围.
的取值范围.
解:(1)原不等式可化为![]() ,
,
![]() ,且
,且![]() ,且
,且![]() ,
,
得![]() .
.
(2)![]() ,
,![]() ,
,
所以![]() 的周期为:4,
的周期为:4,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 定义在
定义在![]() 上的奇函数
上的奇函数![]() ,
,
![]() ,即
,即![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
(3)![]() 关于
关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,
上恒成立,
![]() 记
记![]() ,
,
![]() 关于
关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立,
上恒成立,
当![]() 时,
时,![]() ,
,
![]()
![]() ,即
,即 解得
解得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,即
,即![]() 满足条件;
满足条件;
当![]() 时,
时,![]() ,
,
由![]() 在
在![]() 上恒成立,
上恒成立,
得![]() ,
,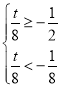 解得
解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震释放出的能量![]() (单位:焦耳)与地震里氏震级
(单位:焦耳)与地震里氏震级![]() 之间的关系为
之间的关系为![]() .
.
(1)已知地震等级划分为里氏![]() 级,根据等级范围又分为三种类型,其中小于
级,根据等级范围又分为三种类型,其中小于![]() 级的为“小地震”,介于
级的为“小地震”,介于![]() 级到
级到![]() 级之间的为“有感地震”,大于
级之间的为“有感地震”,大于![]() 级的为“破坏性地震”若某次地震释放能量约
级的为“破坏性地震”若某次地震释放能量约![]() 焦耳,试确定该次地震的类型;
焦耳,试确定该次地震的类型;
(2)2008年汶川地震为里氏![]() 级,2011年日本地震为里氏
级,2011年日本地震为里氏![]() 级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取
级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=![]() x+4,动圆⊙O:x2+y2=r2(1<r<2),菱形ABCD的一个内角为60°,顶点A、B在直线l上,顶点C、D在⊙O上.当r变化时,求菱形ABCD的面积S的取值范围.
x+4,动圆⊙O:x2+y2=r2(1<r<2),菱形ABCD的一个内角为60°,顶点A、B在直线l上,顶点C、D在⊙O上.当r变化时,求菱形ABCD的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米
千米![]() 小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() 时,每小时的油耗(所需要的汽油量)为
时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以120千米![]() 小时的速度行驶时,每小时的油耗为11.5升,欲使每小时的油耗不超过9升,求
小时的速度行驶时,每小时的油耗为11.5升,欲使每小时的油耗不超过9升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶100千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=ax+1和抛物线y2=4x相交于不同的A,B两点.
(Ⅰ)若a=-2,求弦长|AB|;
(Ⅱ)若以AB为直径的圆经过原点O,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() ,
,![]() ,
,![]() )的部分图像如图所示.
)的部分图像如图所示.
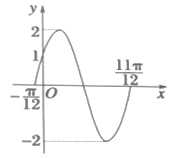
(1)求函数![]() 的解析式及
的解析式及![]() 图像的对称轴方程;
图像的对称轴方程;
(2)把函数![]() 图像上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移
图像上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于x的方程
的图象,求关于x的方程![]() 在
在![]() 时所有的实数根之和.
时所有的实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() ,…,
,…,![]() 是一个数列,对每个
是一个数列,对每个![]() ,
,![]() ,
,![]() .如果
.如果![]() ,
,![]() 两数不同,写
两数不同,写![]() ;如果
;如果![]() ,
,![]() 两数相同,写
两数相同,写![]() .于是得到一个新数列
.于是得到一个新数列![]() ,
,![]() ,…,
,…,![]() ,其中
,其中![]() .重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
.重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
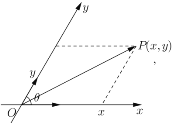
【题目】类似于平面直角坐标系,定义平面斜坐标系:设数轴![]() 、
、![]() 的交点为
的交点为![]() ,与
,与![]() 、
、![]() 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是![]() 、
、![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,其中
,其中![]() ,由平面向量基本定理:对于平面内的向量
,由平面向量基本定理:对于平面内的向量![]() ,存在唯一有序实数对
,存在唯一有序实数对![]() ,使得
,使得![]() ,把
,把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标,也叫做向量
中的坐标,也叫做向量![]() 在斜坐标系
在斜坐标系![]() 中的坐标,记为
中的坐标,记为![]() ,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如![]() 时,方程
时,方程![]() 表示斜坐标系内一条过点
表示斜坐标系内一条过点![]() ,且方向向量为
,且方向向量为![]() 的直线.
的直线.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,已知点
,已知点![]() 和直线
和直线![]() ;
;
①求![]() 的一个法向量;
的一个法向量;
②求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区现有一个直角梯形水产养殖区ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在点P处有一灯塔(如图),且点P到BC,CD的距离都是1200m,现拟将养殖区ACD分成两块,经过灯塔P增加一道分隔网EF,在△AEF内试验养殖一种新的水产品,当△AEF的面积最小时,对原有水产品养殖的影响最小.设AE=d.
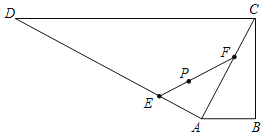
(1)若P是EF的中点,求d的值;
(2)求对原有水产品养殖的影响最小时的d的值,并求△AEF面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com