
【题目】某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分 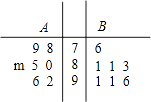
(1)求m的值,并计算A班7名学生成绩的方差s2;
(2)从成绩在90分以上的学生中随机抽取两名学生,求至少有一名A班学生的概率.
【答案】
(1)解:∵A班学生的平均分是85分,
∴ ![]() =85,
=85,
解得m=5,
∴A班7位学生成绩的方差为S2= ![]() [72+112+(﹣5)2+02+02+(﹣7)2+(﹣6)2]=40
[72+112+(﹣5)2+02+02+(﹣7)2+(﹣6)2]=40
(2)解:由茎叶图知成绩在90分以上的学生中,A班有2名,B班有3名,
从成绩在90分以上的学生中随机抽取两名学生,
基本事件总数n= ![]() =10,
=10,
至少有一名A班学生的对立事件是取到的两名学生都是B班学生,
∴至少有一名A班学生的概率p=1﹣ ![]() =
= ![]()
【解析】(1)由A班学生的平均分是85分,能求出m=5,由此能求出A班7位学生成绩的方差.(2)由茎叶图知成绩在90分以上的学生中,A班有2名,B班有3名,从成绩在90分以上的学生中随机抽取两名学生,基本事件总数n为10,至少有一名A班学生的对立事件是取到的两名学生都是B班学生,由此能求出至少有一名A班学生的概率.
【考点精析】本题主要考查了茎叶图的相关知识点,需要掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少才能正确解答此题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1CAC1
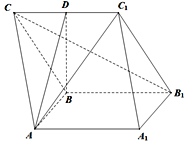
(Ⅰ)求证:平面AA1B1B面BB1C1C;
(Ⅱ)若D是CC1中点,ADB是二面角A-CC1-B的平面角,求直线AC1与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x﹣y+ ![]() =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)求 ![]() 的取值范围;
的取值范围;
(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( ) 
A.f(x)= ![]() sin
sin ![]() x+1,S=2016
x+1,S=2016
B.f(x)= ![]() cos
cos ![]() x+1,S=2016
x+1,S=2016
C.f(x)= ![]() sin
sin ![]() x+1,S=2016.5
x+1,S=2016.5
D.f(x)= ![]() cos
cos ![]() x+1,S=2016.5
x+1,S=2016.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 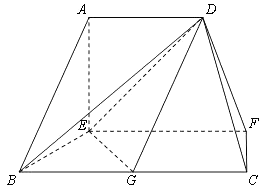
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
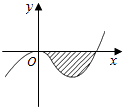
【题目】已知函数f(x)=x3+ax2+bx+c的图像如图,直线y=0在原点处与函数图像相切,且此切线与函数图像所围成的区域(阴影)面积为 ![]() .
. 
(1)求f(x)的解析式
(2)若常数m>0,求函数f(x)在区间[﹣m,m]上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com