
分析 (1)可判断f(x)在[1,+∞)上是增函数,利用导数证明即可.
(2)由f(x)在[1,+∞)上是增函数知在x=1处有最小值.
解答 解:(1)f(x)=$\frac{{x}^{2}+2x+1}{x}$=x+$\frac{1}{x}$+2,
故f(x)在[1,+∞)上是增函数,证明如下,
∵f(x)=x+$\frac{1}{x}$+2,
∴f′(x)=1-$\frac{1}{{x}^{2}}$≥0,
故f(x)在[1,+∞)上是增函数;
(2)∵f(x)在[1,+∞)上是增函数,
∴fmin(x)=f(1)=1=1+2=4.
点评 本题考查了函数的单调性的判断与应用,同时考查了导数的应用.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 若l?α,m不平行于l,则m不平行于α | |
| B. | 若l?α,m?β,且α,β不平行,则l,m不平行 | |
| C. | 若l?α,m不垂直于l,则m不垂直于α | |
| D. | 若l?α,m?β,l不垂直于m,则α,β不垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0=2 | B. | f(x0)=2 | C. | f′(x0)=2 | D. | $\frac{{y}_{0}}{{x}_{0}}$=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
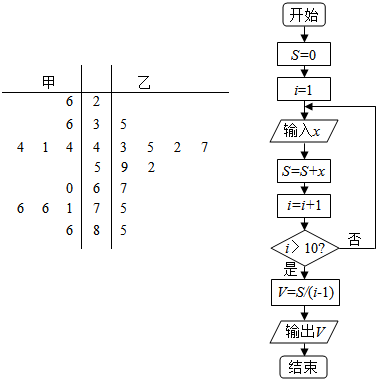 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com