已知



.
(1)
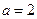
时,求
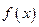
的极值
(2)当
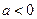
时,讨论
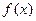
的单调性。
(3)证明:
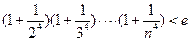
(
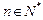
,
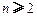
,其中无理数
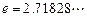
)
解:
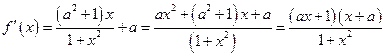
(1)令
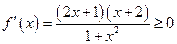
,知
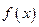
在区间
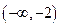
上单调递

增


,
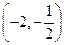
上
单调递减,在
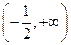
单调递增。
故有极大值
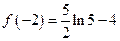
,极小值
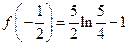
。
(2)当
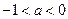
时,
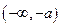
上单调递减,
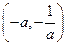
单调递增,
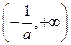
单调递减
当
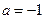
时,
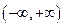
单调递减
当
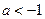
时,
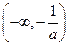
上单调递减,
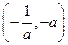
单调递增,
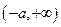
单调递减
(3)由(Ⅰ)当
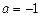
时,
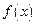
在
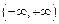
上单调递减。
当

时
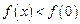
∴
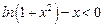

,即
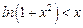
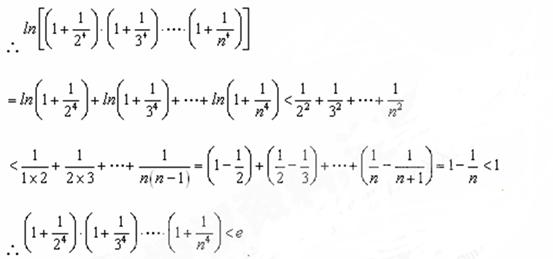
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
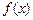
=
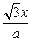
+
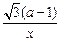
,
a≠0且
a≠1.
(1)试就实数
a的不同取值,写出该函数的单调增区间;
(2)已知当
x>0时,函数在(0,
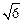
)上单调递减,在(
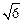
,
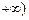
上单调递增,求
a的值并写出函数的解析式;
(3)记(2)中的函数图象为曲线
C,试问是否存在经过原点的直线
l,使得
l为曲线
C的对称轴?若存在,求出直线
l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若曲线
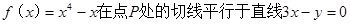
,则点P的坐标为
| A.(1,0) | B.(1,5) | C.(1,  ) ) | D.(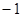 ,2) ,2) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)已知函数
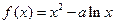
(常数
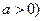
.
(Ⅰ) 当
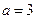
时,求曲线
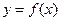
在点
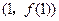
处的切线方程;
(Ⅱ)讨论函数
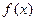
在区间
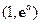
上零点的个数(
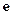
为自然对数的底数).
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

(

)(

为自然对数的底数)
(1)求

的极值
(2)对于数列

,

(

)
① 证明:

② 考察关于正整数


的方程

是否有解,并说明理由
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满

分13分)已知
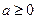
,函数
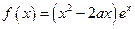
.
(1)当
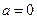
时讨论函数的单调性;
(2)当
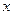
取何值时,
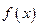
取最小值,证明你的结论.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知函数
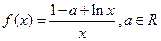
.
(1)求
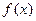
的极值;
(2)若
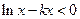
在
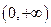
上恒成立,求
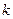
的取值范围;
(3)已知
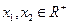
,且
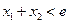
,求证:
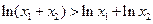
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
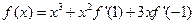
,则
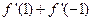
的值为
___▲___.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
不等式
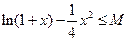
恒成立,则
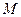
的最小值为 .
查看答案和解析>>



 .
.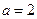 时,求
时,求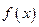 的极值
的极值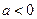 时,讨论
时,讨论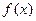 的单调性。
的单调性。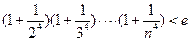 (
(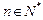 ,
,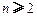 ,其中无理数
,其中无理数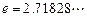 )
)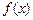 =
=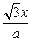 +
+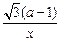 ,a≠0且a≠1.
,a≠0且a≠1.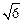 )上单调递减,在(
)上单调递减,在(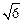 ,
,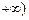 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;