Question

已知函数f（x）=ln（1+x）-ax的图象在x=1处的切线与直线x+2y-1=0平行．
（Ⅰ）求实数a的值；
（Ⅱ）若方程在[2，4]上有两个不相等的实数根，求实数m的取值范围；
（Ⅲ）设常数p≥1，数列{a_n}满足a_n+1=a_n+ln（p-a_n）（n∈N₊），a₁=lnp，求证：a_n+1≥a_n

Answer 1

解：（I ）∵f ′（x）=，
∴f ′（1）=．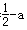
由题知，
解得a=1 ．
（II ）由（I ）有f （x ）=ln （1+x ）-x ，
∴原方程可整理为4ln （1+x ）-x=m ．
令g （x ）=4ln （1+x ）-x ，
得g ′（x）=，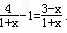
∴当3 ＜x ≤4 时g' （x ）＜0 ，
当2 ≤x ＜3 时g' （x ）＞0 ，g' （3 ）=0 ，
即g （x ）在[2 ，3] 上是增函数，在[3 ，4] 上是减函数，
∴在x=3 时g （x ）有最大值4ln4-3 ．
∵g （2 ）=4ln3-2 ，
g （4 ）=4ln5-4 ，
∴g （2 ）-g （4 ）=．
由9e ≈24.46 ＜25 ，
于是
∴g （2 ）＜g（4 ）．
∴a 的取值范围为[4ln5-4 ，4ln4-3 ）
（III ）由f （x ）=ln （1+x ）-x （x ＞-1 ）
有f ′（x）=，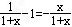
显然f' （0 ）=0 ，
当x ∈（0 ，+ ∞）时，f' （x ）＜0 ，
当x ∈（-1 ，0 ）时，f' （x ）＞0 ，
∴f （x ）在（-1 ，0 ）上是增函数，在[0 ，+ ∞）上是减函数．
∴f （x ）在（-1 ，+ ∞）上有最大值f （0 ），
而f （0 ）=0 ，
∴当x ∈（-1 ，+ ∞）时，f （x ）≤0 ，
因此ln （1+x ）≤x（* ）
由已知有p ＞a_n ，
即p-a_n ＞0 ，
所以p-a _n-1 ＞-1 ．
∵a_n+1-a_n=ln （p-a_n ）=ln （1+p-1-a_n ），
∴由（* ）中结论可得a  _n+1-a_n ≤p-1-a_n ，
即a_n+1 ≤p-1 （n ∈N* ）．
∴当n ≥2 时，a_n+1-a_n=ln （p-a_n ）≥ln[p- （p-1 ）]=0 ，
即a_n+1≥a_n ．
当n=1 ，a₂=a₁+ln （p-lnp ），
∵lnp=ln （1+p-1 ）≤p-1 ，
∴a₂ ≥a₁+ln[p- （p-1 ）]=a₁，
结论成立．
∴对n ∈N* ，a_n+1≥a_n。