
A、若|
| ||||||||||||||||
B、
| ||||||||||||||||
C、若△ABC中,a=5,b=8,c=7,则
| ||||||||||||||||
D、若非零向量
|
| a |
| b |
| a |
| b |
| 1 |
| 5 |
| 1 |
| 2 |
| BC |
| CA |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 5 |
| 1 |
| 2 |
| BC |
| CA |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源:2012-2013学年辽宁省铁岭市六校协作高三第一次联合考试理科数学试卷(解析版) 题型:选择题
已知函数 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )
A.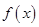 既不是奇函数,也不是偶函数 B.
既不是奇函数,也不是偶函数 B.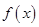 在
在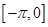 上恰有一个零点
上恰有一个零点
C.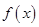 是周期函数 D.
是周期函数 D.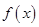 在
在 上是增函数
上是增函数
查看答案和解析>>
科目:高中数学 来源:梅州一模 题型:单选题
| A.?x>0,有ln2x+lnx+1>0 |
| B.?α,β∈R,使cos(α+β)=cosα+cosβ |
| C.“a2<b2”是“a<b”的必要不充分条件 |
| D.?m∈R,使f(x)=(m-1)xm2-4m+3是幂函数,且在(0,+∞)上递减 |
查看答案和解析>>
科目:高中数学 来源:2012年辽宁省营口市高三数学试卷(解析版) 题型:选择题
 的双曲线的两条渐近线互相垂直
的双曲线的两条渐近线互相垂直 垂直的直线方程是2x+y-3=0
垂直的直线方程是2x+y-3=0 的两条准线之间的距离为
的两条准线之间的距离为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com