解:∵x
2-2x-15≥0?(x-5)(x+3)≥0?x≤-3或x≥5
∴集合A={x|x
2-2x-15≥0}=(-∞,-3]∪[5,+∞)
而|x-2k|<1等价于-1<x-2k<1,可得2k-1<x<2k+1
∴集合B={x||x-2k|<1}=(2k-1,2k+1)
(I)A∩B=∅,可得
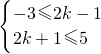
?-1≤k≤2;
∴实数k的取值范围是[-1,2]
(II)B⊆A,可得(2k-1,2k+1)⊆(-∞,-3]或(2k-1,2k+1)⊆[5,+∞)
①当(2k-1,2k+1)⊆(-∞,-3]时,2k+1≤-3,可得k≤-2
②当(2k-1,2k+1)⊆[5,+∞)时,2k-1≥5,可得k≥3
综上,实数k的取值范围是(-∞,-2]∪[3,+∞);
(III)当且仅当
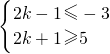
时,A∪B=R成立
此时k≤-1且k≥2矛盾,所以不存在实数k使A∪B=R成立.
分析:先根据一元二次不等式解法与绝对值不等式解法的结论,将集合A、B进行化简,得到A=(-∞,-3]∪[5,+∞),B=(2k-1,2k+1)
(I)若A∩B=∅,说明不存在元素x使x∈A且x∈B同时成立,因此有-3≤2k-1<2k+1≤5,从而找到实数k的取值范围;
(II)若B⊆A成立,说明(2k-1,2k+1)是区间(-∞,-3]的子集,或(2k-1,2k+1)是区间[5,+∞)的子集,因此分两种情况加以讨论,可得实数k的取值范围;
(III)先假设存在实数k使A∪B=R,通过建立不等式组
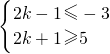
,得到k值既要小于或等于-1又要大于或等于2,出现矛盾,从而说明不存在满足条件的实数k.
点评:本题以一元二次不等式解法和含有绝对值不等式解法为载体,考查了集合关系中的参数取值问题,属于基础题.

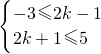 ?-1≤k≤2;
?-1≤k≤2;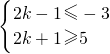 时,A∪B=R成立
时,A∪B=R成立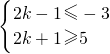 ,得到k值既要小于或等于-1又要大于或等于2,出现矛盾,从而说明不存在满足条件的实数k.
,得到k值既要小于或等于-1又要大于或等于2,出现矛盾,从而说明不存在满足条件的实数k.
