Question

如图，ABCD是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，∠PDA＝45°，

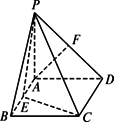
(1)求证：AF∥平面PEC；

(2)求证：平面PEC⊥平面PCD；

(3)若AD＝1，CD＝，求点A到平面PEC的距离．

Answer 1

答案：
解析：

(1)证明：取PC中点H，连FH得FH∥CD， 　　且FH＝CD． 　　又∵AE＝CD， 　　∴AE＝FH，即AEHF是平行四边形． 　　∴AF∥EH，∵AF平面PEC，HE平面PEC， 　　∴AF∥平面PEC． 　　(2)证明：∵ABCD是矩形且PA⊥底面ABCD，∴CD⊥平面PAD． 　　∴CD⊥AF． 　　∵PA⊥AD，∠PDA＝45°，F是PD中点． 　　∴AF⊥PD． 　　∴AF⊥平面PCD， 　　又∵HE∥AF，∴HE⊥平面PCD． 　　∵HE面PEC， 　　∴平面PEC⊥平面PCD． 　　(3)解：∵AF∥平面PEC，∴点A到平面PEC之距即为点F到平面PEC之距． 　　∵平面PEC⊥平面PCD， 　　在平面PCD内过F作PC的垂线FK交PC于K． 　　则FK⊥平面PEC，即点F到平面PEC的距离为FK． 　　由PA⊥AD，∠PDA＝45°知PD＝． 　　又CD＝，CD⊥PD，∴△PCD斜边上的高为1． 　　∴FK＝． 　　∴点A到平面PEC的距离为．