
设奇函数 上是增函数,且
上是增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( )
A.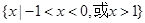 | B.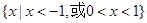 |
C. | D. |
D
解析试题分析:由题意可知,函数f(x)是奇函数,函数f(x)在(0,+∞)上是增函数,∴它在(-∞,0)上也是增函数.∵f(-x)=-f(x),∴f(-1)=f(1)=0.不等式x[f(x)-f(-x)]<0可化为2xf(x)<0,即xf(x)<0,∴当x<0时,可得f(x)>0=f(-1),∴x>-1,∴-1<x<0;当x>0时,可得f(x)<0=f(1),∴x<1,∴0<x<1.综上,
不等式x[f(x)-f(-x)]<0的解集为{x|-1<x0,或0<x<1}.故选D.
考点:本试题主要考查了是函数的奇偶性和单调性以及解不等式的综合类问题.在解答的过程当中充分体现了转化的思想、数形结合的思想以及函数单调性与奇偶性的知识.值得同学们体会和反思.
点评:解决该试题的关键要结合奇偶性和单调性对不等式进行转化变形,将问题转化为解不等式:2xf(x)<0,然后再分类讨论即可获得问题的解答。


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:单选题
对实数a和b,定义运算“⊕”:a⊕b= 设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B.(-∞,-2]∪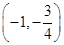 |
C.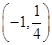 ∪ ∪ | D.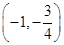 ∪ ∪ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,液体从一圆锥漏斗漏入一圆柱桶中,开始漏斗盛满液体,经过3分钟漏完,若圆柱中液面上升速度是一常量, H是圆锥漏斗中液面下落的距离. 则H与下落时间t分钟的函数关系表示的图象可能是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com