
分析:本题可用对称的实质即直线AB与l垂直,线段AB的中点在l上,联立直线AB与椭圆方程利用判别式求解;又因存在关于l对称的两点A、B,所以AB的中点在l上,由直线AB与直线l垂直,知kAB=![]() ,故可用“点差法”求出AB中点M的坐标,然后利用点M在椭圆内部去求解.
,故可用“点差法”求出AB中点M的坐标,然后利用点M在椭圆内部去求解.
解:设A(x1,y1),B(x2,y2),AB的中点M(x0,y0).
则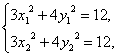
两式相减得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
即![]() .
.
所以y0=3x0.又M(x0,y0)在直线l上,
所以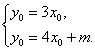
解得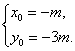
因为点M(-m,-3m)在椭圆内部,
所以3(-m)2+4(-3m)2<12,
即![]() .
.
所以m的取值范围为m∈(![]() ,
,![]() ).
).


科目:高中数学 来源:选修设计数学1-1北师大版 北师大版 题型:044
已知椭圆C:3x2+4y2=12,试确定m的取值范围,使得对于直线l:y=4x+m,椭圆上有不同的两点A、B关于这条直线对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com