
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1) 取![]() 的中点
的中点![]() ,连结
,连结![]() ,
, ![]() ,由题意证得
,由题意证得![]() ∥
∥![]() ,利用线面平行的判断定理即可证得结论;(2)建立空间直角坐标系,求得半平面的法向量:
,利用线面平行的判断定理即可证得结论;(2)建立空间直角坐标系,求得半平面的法向量: ![]() ,
, ![]() ,然后利用空间向量的相关结论可求得二面角
,然后利用空间向量的相关结论可求得二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:(1)取![]() 中点
中点![]() ,连结
,连结![]() ,
, ![]() .
.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
, ![]() ,由
,由![]() 得
得![]() ,又
,又![]()
所以![]() .四边形
.四边形![]() 为平行四边形,
为平行四边形, ![]() .
.
又![]() ,
, ![]() ,故
,故![]()
(2)
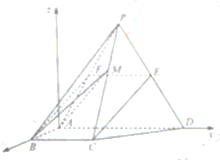
由已知得![]() ,以A为坐标原点,
,以A为坐标原点, ![]() 的方向为x轴正方向,
的方向为x轴正方向, ![]() 为单位长,建立如图所示的空间直角坐标系A-xyz,则
为单位长,建立如图所示的空间直角坐标系A-xyz,则
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() 则
则
![]()
因为BM与底面ABCD所成的角为45°,而![]() 是底面ABCD的法向量,所以
是底面ABCD的法向量,所以
![]() ,
, 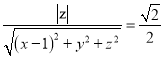
即(x-1)+y-z=0
又M在棱PC上,学|科网设![]()
![]()
由①,②得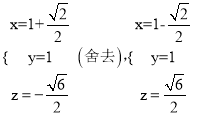
所以M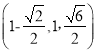 ,从而
,从而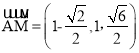
设![]() 是平面ABM的法向量,则
是平面ABM的法向量,则
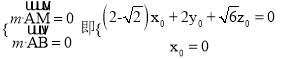
所以可取m=(0,-![]() ,2).于是
,2).于是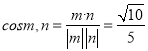
因此二面角M-AB-D的余弦值为![]()
点睛:(1)求解本题要注意两点:①两平面的法向量的夹角不一定是所求的二面角,②利用方程思想进行向量运算,要认真细心、准确计算.
(2)设m,n分别为平面α,β的法向量,则二面角θ与<m,n>互补或相等,故有|cos θ|=|cos<m,n>|=![]() .求解时一定要注意结合实际图形判断所求角是锐角还是钝角.
.求解时一定要注意结合实际图形判断所求角是锐角还是钝角.


科目:高中数学 来源: 题型:
【题目】小图给出了某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() (月)的关系的散点图.有以下叙述:
(月)的关系的散点图.有以下叙述:

①与函数![]() 相比,函数
相比,函数![]() 作为近似刻画
作为近似刻画![]() 与
与![]() 的函数关系的模型更好;
的函数关系的模型更好;
②按图中数据显现出的趋势,第![]() 个月时,浮萍的面积就会超过
个月时,浮萍的面积就会超过![]() ;
;
③按图中数据显现出的趋势,浮萍每个月增加的面积约是上个月增加面积的两倍;
④按图中数据显现出的趋势,浮萍从![]() 月的
月的![]() 蔓延到
蔓延到![]() 至少需要经过
至少需要经过![]() 个月.
个月.
其中正确的说法有__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为及时了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位30岁到40岁的公务员,得到情况如表:
(1)完成表格,并判断是否有99%以上的把握认为“生二胎意愿与性别有关”,并说明理由;
(2)现把以上频率当作概率,若从社会上随机独立抽取三位30岁到40岁的男公务员访问,求这三人中至少有一人有意愿生二胎的概率.
(3)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省女联的人数为X,求X的公布列及数学期望E(X).
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 30 | 15 | |
无意愿生二胎 | 20 | 25 | |
总计 |
附: ![]()
P(k2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程
(2)若直线l的极坐标方程为ρ(sinθ+cosθ)=1,求直线l被曲线C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]()
![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奥地利遗传学家孟德尔1856年用豌豆作实验时,他选择了两种性状不同的豌豆,一种是子叶颜色为黄色,种子性状为圆形,茎的高度为长茎,另一种是子叶颜色为绿色,种子性状为皱皮,茎的高度为短茎。我们把纯黄色的豌豆种子的两个特征记作![]() ,把纯绿色的豌豆的种子的两个特征记作
,把纯绿色的豌豆的种子的两个特征记作![]() ,实验杂交第一代收获的豌豆记作
,实验杂交第一代收获的豌豆记作![]() ,第二代收获的豌豆出现了三种特征分别为
,第二代收获的豌豆出现了三种特征分别为![]() ,
,![]() ,
,![]() ,请问,孟德尔豌豆实验第二代收获的有特征
,请问,孟德尔豌豆实验第二代收获的有特征![]() 的豌豆数量占总收成的( )
的豌豆数量占总收成的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)的影响,对近六年的年宣传费
(单位:吨)的影响,对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣传费 | 23 | 25 | 27 | 29 | 32 | 35 |
年销售量 | 11 | 21 | 24 | 66 | 115 | 325 |
(1)根据散点图判断![]() 与
与![]() ,哪一个更适合作为年销售量
,哪一个更适合作为年销售量![]() (吨)与关于宣传费
(吨)与关于宣传费![]() (万元)的回归方程类型;
(万元)的回归方程类型;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为
(万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为![]() ,试求
,试求![]() 的所有取值情况及对应的概率;
的所有取值情况及对应的概率;
(3)根据频率分布直方图中求出样本数据平均数的思想方法,求![]() 的平均数.
的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com