练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】阿波罗尼斯（约公元前年）证明过这样一个命题:平面内到两定点距离之比为常数的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.若平面内两定点、间的距离为，动点满足，则的最小值为（ ）

    A. B. C. D.

    【答案】A

    【解析】

    以经过、的直线为轴，线段的垂直平分线轴，建立直角坐标系，得出点、的坐标，设点，利用两点间的距离公式结合条件得出点的轨迹方程，然后利用坐标法计算出的表达式，再利用数形结合思想可求出的最小值.

    以经过、的直线为轴，线段的垂直平分线轴，建立直角坐标系，

    则、，设，，，

    两边平方并整理得，

    所以点的轨迹是以为圆心，为半径的圆，

    则有，如下图所示：

    当点为圆与轴的交点（靠近原点）时，此时，取最小值，且，

    因此，，故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列｛｝的前n项和为Sn，，且对任意的n∈N*，n≥2都有。

    （1）若0，，求r的值；

    （2）数列｛｝能否是等比数列？说明理由；

    （3）当r＝1时，求证：数列｛｝是等差数列。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设.

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）当时，在内是否存在一实数，使成立？请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,是平行四边形，已知，,平面平面.

    （1）证明：；

    （2）若，求平面与平面所成二面角的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中老年人群体中，肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系，调查了50位中老年人每周运动的总时长（单位：小时），将数据分成[0，4），[4，8），[8，14），[14，16），[16，20），[20，24]6组进行统计，并绘制出如图所示的柱形图．

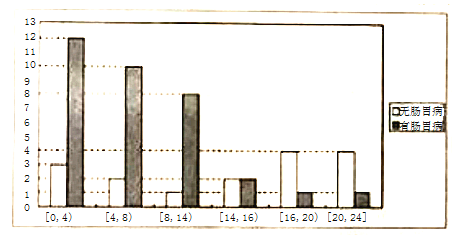
    图中纵轴的数字表示对应区间的人数现规定：每周运动的总时长少于14小时为运动较少．

    每周运动的总时长不少于14小时为运动较多．

    （1）根据题意，完成下面的2×2列联表：

    有肠胃病

    无肠胃病

    总计

    运动较多

    运动较少

    总计

    （2）能否有99.9%的把握认为中老年人是否有肠胃病与运动有关？

    附：K2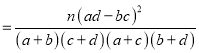（n＝a+b+c+d）

    P（K2≥k）

    0.0.50

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中，为自然对数的底数.

    （1）求函数的单调递增区间；

    （2）当时，，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家电公司销售部门共有200位销售员，每位部门对每位销售员都有1400万元的年度销售任务，已知这200位销售员去年完成销售额都在区间（单位：百万元）内，现将其分成5组，第1组，第2组，第3组，第4组，第5组对应的区间分别为， ， ， ， ，绘制出频率分布直方图.

    （1）求的值，并计算完成年度任务的人数；

    （2）用分层抽样从这200位销售员中抽取容量为25的样本，求这5组分别应抽取的人数；

    （3）现从（2）中完成年度任务的销售员中随机选取2位，奖励海南三亚三日游，求获得此奖励的2位销售员在同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某社区消费者协会为了解本社区居民网购消费情况，随机抽取了100位居民作为样本，就最近一年来网购消费金额(单位：千元)，网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间内，按，，，，，分成6组，其频率分布直方图如图所示.

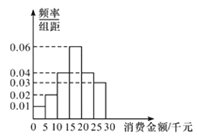
    （1）估计该社区居民最近一年来网购消费金额的中位数；

    （2）将网购消费金额在20千元以上者称为“网购迷”，补全下面的列联表，并判断有多大把握认为“网购迷与性别有关系”；

    男

    女

    合计

    网购迷

    20

    非网购迷

    45

    合计

    100

    （3）调査显示，甲、乙两人每次网购采用的支付方式相互独立，两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式，所得数据如下表所示：

    网购总次数

    支付宝支付次数

    银行卡支付次数

    微信支付次数

    甲

    80

    40

    16

    24

    乙

    90

    60

    18

    12

    将频率视为概率，若甲、乙两人在下周内各自网购2次，记两人采用支付宝支付的次数之和为，求的数学期望.

    附：观测值公式：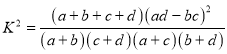

    临界值表：

    0.01

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：

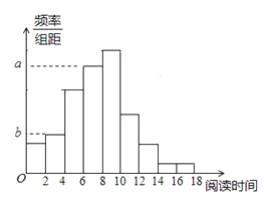
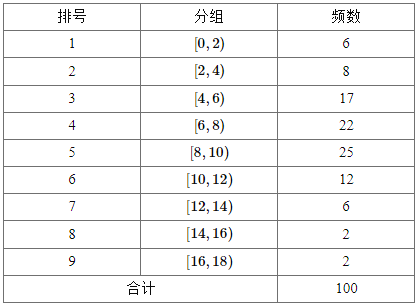
    （1）求频率分布直方图中的，的值；

    （2）从阅读时间在的学生中任选2人，求恰好有1人阅读时间在，另1人阅读时间在的概率.

    查看答案和解析>>

    同步练习册答案