
【题目】对某校高三年级100名学生的视力情况进行统计(如果两眼视力不同,取较低者统计),得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
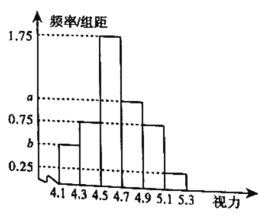
(1)求a,b的值;
(2)若报考高校A专业的资格为:任何一眼裸眼视力不低于5.0,已知在![]() 中有
中有![]() 的学生裸眼视力不低于5.0.现用分层抽样的方法从
的学生裸眼视力不低于5.0.现用分层抽样的方法从![]() 和
和![]() 中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的右焦点为F(3,0),左、右顶点分别为M,N,点P是E在第一象限上的任意一点,且满足kPMkPN=8.
(a>0,b>0)的右焦点为F(3,0),左、右顶点分别为M,N,点P是E在第一象限上的任意一点,且满足kPMkPN=8.
(1)求双曲线E的方程;
(2)若直线PN与双曲线E的渐近线在第四象限的交点为A,且△PAF的面积不小于3![]() ,求直线PN的斜率k的取值范围.
,求直线PN的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 将圆
将圆![]() 的圆周分为四等份,且椭圆
的圆周分为四等份,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)
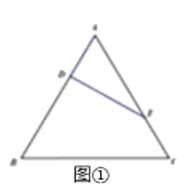
等边△ABC的边长为3,点D,E分别为AB,AC上的点,且满足![]() (如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
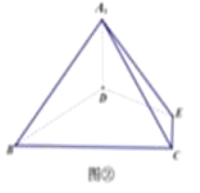
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P(不包括端点),使直线PA1与平面A1BD所成的角为60°?若存在,求出A1P的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数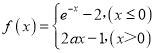 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题:
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③若f(x)>0在![]() 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1;
④对任意的x1<0,x2<0且x1≠x2,恒有
![]() .
.
其中正确命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,已知椭圆的长轴为
的左、右焦点,已知椭圆的长轴为![]() 是椭圆
是椭圆![]() 上一动点,
上一动点,![]() 的最大值为
的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,其中
,其中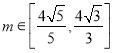 ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
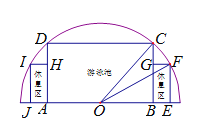
【题目】如图,有一块半圆形空地,开发商计划建造一个矩形游泳池![]() 及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为
及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形
,矩形![]() 的一边
的一边![]() 在
在![]() 上,矩形
上,矩形![]() 的一边
的一边![]() 在
在![]() 上,点
上,点![]() 在圆周上,
在圆周上,![]() 在直径上,且
在直径上,且![]() ,设
,设![]() .若每平方米游泳池的造价与休息区造价之比为
.若每平方米游泳池的造价与休息区造价之比为![]() .
.
(1)记游泳池及休息区的总造价为![]() ,求
,求![]() 的表达式;
的表达式;
(2)为进行投资预算,当![]() 为何值时,总造价最大?并求出总造价的最大值.
为何值时,总造价最大?并求出总造价的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com