练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设f (x)是定义在R上的奇函数，且y= f (x)的图像关于直线x=对称，则f(1)+ f (2)+f (3)+

    f (4) +f (5)=__ ___．

    0；分析：；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设f(x)是定义在A上的减函数，且f(x)＞0，则下列函数中为增函数的个数是(    )

    ①y=3-f(x)  ②y=1＋  ③y=［f(x)］2  ④y=1-

    A.1               B.2                C.3               D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(x)是定义在R上,以2为周期的周期函数,当x∈(-1,1］时,f(x)=x2.求:

           (1)当x∈(1,3］时,f(x)的表达式；

           (2)f(-3)及f(3.5)的值.

          

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(x)是定义在R上的以3为周期的奇函数，若f(1)＞1，f(2)=，则实数a的取值范围是(    )

    A．a＜-1或a＞                       B．-l＜a＜

    C．a＜                                  D．a＜且a≠-1

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年大纲版高三上学期单元测试（6）数学试卷 题型：解答题

    设f(x)是定义在［－1，1］上的奇函数，且对任意的实数a,b∈［－1,1］,当a+b

    ≠0时，都有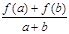>0.

     

    （1）若a>b,试比较f(a)与f(b)的大小;

    （2）解不等式f(x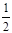－)<f(x－);

     

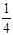    （3）如果g(x)=f(x－c)和h(x)=f(x－c2)这两个函数的定义域的交集是空集，求c的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：江苏省2010年高考预测试题数学 题型：解答题

    设f(x)是定义在[0,1]上的函数，若存在x*∈(0，1)，使得f(x)在[0，x*]上单调递增，在[x*，1]上单调递减，则称f(x)为[0，1]上的单峰函数，x*为峰点，包含峰点的区间为含峰区间．对任意的[0，1]上的单峰函数f(x)，下面研究缩短其含峰区间长度的方法．

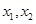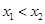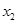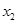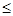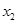      (I)证明：对任意的∈(O，1)，，若f()≥f()，则(0，)为含峰区间：若f()f()，则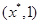为含峰区间：

      (II)对给定的r(0<r<0.5)，证明：存在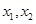∈(0，1)，满足，使得由(I)所确定的含峰区间的长度不大于0.5+r：

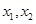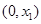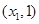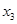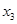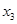      (III)选取∈(O，1)，，由(I)可确定含峰区间为或，在所得的含峰区间内选取，由与或与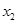类似地可确定一个新的含峰区间，在第一次确定的含峰区间为（0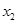，）的情况下，试确定的值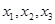，满足两两之差的绝对值不小于0.02，且使得新的含峰区间的长度缩短到0. 34（区间长度等于区间的右端点与左端点之差）

     

    查看答案和解析>>

    同步练习册答案