
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别是
,左、右焦点分别是![]() 、
、![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的短半轴为半径的圆与直线
的短半轴为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 上不在
上不在![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 的平行线交椭圆与
的平行线交椭圆与![]() 、
、![]() 两个不同的点,记
两个不同的点,记![]() ,
,![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】某工厂为生产一种精密管件研发了一台生产该精密管件的车床,该精密管件有内外两个口径,监管部门规定“口径误差”的计算方式为:管件内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() 则“口径误差”为
则“口径误差”为![]() 只要“口径误差”不超过
只要“口径误差”不超过![]() 就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
(Ⅰ)以上述样本的频率作为概率,在昼夜两个批次中分别抽取2件产品,求其中恰有1件不合格产品的概率;
(Ⅱ)若每批次各生产1000件,已知每件产品的成本为5元,每件合格品的利润为10元;若对产品检验,则每件产品的检验费用为2.5元;若有不合格品进入用户手中,则工厂要对用户赔偿,这时生产的每件不合格品工厂要损失25元.以上述样本的频率作为概率,以总利润的期望值为决策依据,分析是否要对每个批次的所有产品作检测?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,圆
为坐标原点,圆![]() :
:![]() ,定点
,定点![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 的半径
的半径![]() 于点
于点![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)不垂直于![]() 轴且不过
轴且不过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 、
、![]() 的斜率之和为0,则动直线
的斜率之和为0,则动直线![]() 是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.
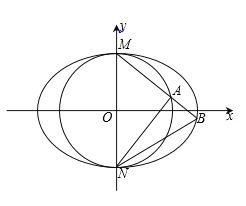
(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无线电技术在航海中有很广泛的应用,无线电波可以作为各种信息的载体.现有一艘航行中的轮船需要与陆地上的基站进行通信,其连续向基站拍发若干次呼叫信号,每次呼叫信号被基站收到的概率都是0.2,基站收到呼叫信号后立即向轮船拍发回答信号,回答信号一定能被轮船收到.
(Ⅰ)若要保证基站收到信号的概率大于0.99,求轮船至少要拍发多少次呼叫信号.
(Ⅱ)设(Ⅰ)中求得的结果为![]() .若轮船第一次拍发呼叫信号后,每隔5秒钟拍发下一次,直到收到回答信号为止,已知该轮船最多拍发
.若轮船第一次拍发呼叫信号后,每隔5秒钟拍发下一次,直到收到回答信号为止,已知该轮船最多拍发![]() 次呼叫信号,且无线电信号在轮船与基站之间一个来回需要16秒,设轮船停止拍发时,一共拍发了
次呼叫信号,且无线电信号在轮船与基站之间一个来回需要16秒,设轮船停止拍发时,一共拍发了![]() 次呼叫信号,求
次呼叫信号,求![]() 的数学期望(结果精确到0.01).
的数学期望(结果精确到0.01).
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两动圆![]() 和
和![]() (
(![]() ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线![]() ,若曲线
,若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 满足:
满足:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)证明直线![]() 恒经过一定点,并求此定点的坐标;
恒经过一定点,并求此定点的坐标;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,直线
,直线![]() 过
过![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.![]() 到准线的距离之和最小为8.
到准线的距离之和最小为8.
(1)求抛物线方程;
(2)若抛物线上一点![]() 纵坐标为
纵坐标为![]() ,直线
,直线![]() 分别交准线于
分别交准线于![]() .求证:以
.求证:以![]() 为直径的圆过焦点
为直径的圆过焦点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com