
【题目】已知![]() R,函数
R,函数![]() =
=![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() >1;
>1;
(2)若关于![]() 的方程
的方程![]() +
+![]() =0的解集中恰有一个元素,求
=0的解集中恰有一个元素,求![]() 的值;
的值;
(3)设![]() >0,若对任意
>0,若对任意![]()
![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18-![]() ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=![]() (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 过坐标原点
过坐标原点![]() 且圆心在曲线
且圆心在曲线![]() 上.
上.
(1)若圆![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() (不同于原点
(不同于原点![]() ),求证:
),求证:![]() 的面积为定值;
的面积为定值;
(2)设直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求圆
,求圆![]() 的方程;
的方程;
(3)设直线![]() 与(2)中所求圆
与(2)中所求圆![]() 交于点
交于点![]() 、
、![]() ,
, ![]() 为直线
为直线![]() 上的动点,直线
上的动点,直线![]() ,
,![]() 与圆
与圆![]() 的另一个交点分别为
的另一个交点分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 在直线
在直线![]() 异侧,求证:直线
异侧,求证:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中有高一新生500名,分成水平相同的![]() 两类教学实验,为对比教学效果,现用分层抽样的方法从
两类教学实验,为对比教学效果,现用分层抽样的方法从![]() 两类学生中分别抽取了40人,60人进行测试
两类学生中分别抽取了40人,60人进行测试
(1)求该学校高一新生![]() 两类学生各多少人?
两类学生各多少人?
(2)经过测试,得到以下三个数据图表:
图1:75分以上![]() 两类参加测试学生成绩的茎叶图
两类参加测试学生成绩的茎叶图
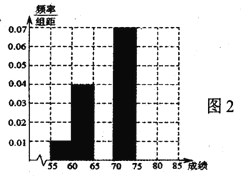
图2:100名测试学生成绩的频率分布直方图
下图表格:100名学生成绩分布表:
①先填写频率分布表中的六个空格,然后将频率分布直方图(图2)补充完整;
②该学校拟定从参加考试的79分以上(含79分)的![]() 类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),
(纵坐标不变),
得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com