
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,点
,点![]() ,
,![]() 在该抛物线上且位于
在该抛物线上且位于![]() 轴的两侧,
轴的两侧,![]() .
.
(Ⅰ)证明:直线![]() 过定点
过定点![]() ;
;
(Ⅱ)以![]() ,
,![]() 为切点作
为切点作![]() 的切线,设两切线的交点为
的切线,设两切线的交点为![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)证明见解析;(Ⅱ)2.
【解析】
(Ⅰ)先求出抛物线的方程,然后设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() (
(![]() ,
,![]() ),联立直线和抛物线的方程可得
),联立直线和抛物线的方程可得![]() ,由韦达定理可得
,由韦达定理可得![]() 的值,再根据
的值,再根据![]() ,可得出b的值,进而可得出直线恒过定点;
,可得出b的值,进而可得出直线恒过定点;
(Ⅱ)以![]() 为切点的切线方程为
为切点的切线方程为![]() ,以
,以![]() 为切点的切线方程为
为切点的切线方程为![]() ,联立
,联立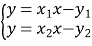 ,解得
,解得![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,所以两切线交点
,所以两切线交点![]() 的轨迹方程为
的轨迹方程为![]() ,进而可得出
,进而可得出![]() 的最小值.
的最小值.
(Ⅰ)根据题意,![]() ,所以
,所以![]() .
.
故抛物线![]() .
.
由题意设直线![]() 的方程为
的方程为![]() .
.
由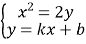 ,消去
,消去![]() 整理得
整理得![]() .
.
显然![]() .
.
设![]() ,
,![]() (
(![]() ,
,![]() ),则
),则![]() ,
,
所以![]() .
.
由题意得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
所以直线![]() 的方程为
的方程为![]() ,故直线
,故直线![]() 过定点
过定点![]() ;
;
(Ⅱ)因为![]() ,所以
,所以![]() ,
,![]() ,
,
故以![]() 为切点的切线方程为
为切点的切线方程为![]() ,即
,即![]() ,
,
以![]() 为切点的切线方程为
为切点的切线方程为![]() ,即
,即![]()
联立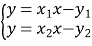 ,解得
,解得![]() .
.
又因为![]() ,
,
所以两切线交点![]() 的轨迹方程为
的轨迹方程为![]() .
.
因为圆心到直线![]() 的距离为3,
的距离为3,
所以圆上一点到直线![]() 的最小距离为
的最小距离为![]() ,
,
故![]() 的最小值为2.
的最小值为2.


科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
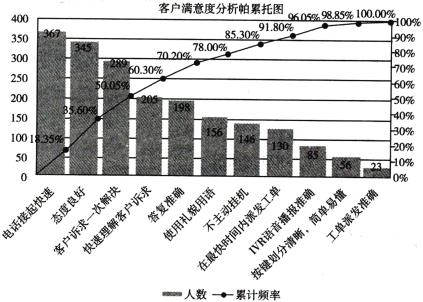
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: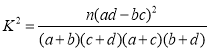 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考前回归课本复习过程中,一数学老师在黑板上写了下面四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .然后说了四句话:第一句:“该函数定义域为
.然后说了四句话:第一句:“该函数定义域为![]() ,还是奇函数”.第二句:“该函数为偶函数,值域不是
,还是奇函数”.第二句:“该函数为偶函数,值域不是![]() ”.第三句:“该函数定义域为
”.第三句:“该函数定义域为![]() ,还是单调函数”.第四句:“该函数的图象有对称轴,值域是
,还是单调函数”.第四句:“该函数的图象有对称轴,值域是![]() ”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“垛积术”是我国古代数学的重要成就之一.南宋数学家杨辉在《详解九章算法》中记载了“方垛”的计算方法:“果子以垛,下方十四个,问计几何?术曰:下方加一,乘下方为平积.又加半为高,以乘下方为高积.如三而一.”意思是说,将果子以方垛的形式摆放(方垛即每层均为正方形,自下而上每层每边果子数依次递减1个,最上层为1个),最下层每边果子数为14个,问共有多少个果子?计算方法用算式表示为![]() .利用“方垛”的计算方法,可计算最下层每边果子数为14个的“三角垛”(三角垛即每层均为正三角形,自下而上每层每边果子数依次递减1个,最上层为1个)共有果子数为( )
.利用“方垛”的计算方法,可计算最下层每边果子数为14个的“三角垛”(三角垛即每层均为正三角形,自下而上每层每边果子数依次递减1个,最上层为1个)共有果子数为( )
A.420个B.560个C.680个D.1015个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
A 71 62 72 76 63 70 85 83
B 73 84 75 73 7![]() 8
8![]() 76 85
76 85
B同学的成绩不慎被墨迹污染(![]() ,
,![]() 分别用m,n表示).
分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A、B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差![]() ,求m,n.
,求m,n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com