
【题目】已知函数f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函数f(x)的图象在x=1处的切线与x轴平行,求f(x)的单调区间;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范围.
,+∞)上恒成立,求a的取值范围.
【答案】(1)单调递增区间为(0,+∞),无单调递减区间.(2)-4-4ln 2≤a<0.
【解析】
(1) f '(x)=![]() +2ax-2由f '(1)=1+2a-2=0,解得a=
+2ax-2由f '(1)=1+2a-2=0,解得a=![]() ,得f '(x)=
,得f '(x)=![]() ≥0恒成立,则单调区间可求;(2) f(x)≤ax转化为ln x+ax2-2x-ax≤0,构造函数g(x)=ln x+ax2-2x-ax,x∈[
≥0恒成立,则单调区间可求;(2) f(x)≤ax转化为ln x+ax2-2x-ax≤0,构造函数g(x)=ln x+ax2-2x-ax,x∈[![]() ,+∞),求导求其最大值即可求解
,+∞),求导求其最大值即可求解
(1)函数f(x)=ln x+ax2-2x,定义域为(0,+∞),f '(x)=![]() +2ax-2.
+2ax-2.
由已知f '(1)=1+2a-2=0,解得a=![]() ,
,
于是f '(x)=![]() ≥0恒成立,
≥0恒成立,
从而f(x)的单调递增区间为(0,+∞),无单调递减区间.
(2) f(x)≤ax转化为ln x+ax2-2x-ax≤0,
设g(x)=ln x+ax2-2x-ax,x∈[![]() ,+∞),
,+∞),
则g'(x)=![]() +2ax-2-a=
+2ax-2-a=![]() .
.
①当a<0时,g(x)在[![]() ,+∞)上单调递减,
,+∞)上单调递减,
因而g(![]() )=ln
)=ln![]() +
+![]() a-1-
a-1-![]() a≤0,故-4-4ln 2≤a<0;
a≤0,故-4-4ln 2≤a<0;
②当0<a<2时,![]() ,g(x)在[
,g(x)在[![]() ,
,![]() ]上单调递减,在(
]上单调递减,在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
因而g(x)∈[g(![]() ),+∞),不符合题意;
),+∞),不符合题意;
③当a≥2时,![]() ,g(x)在[
,g(x)在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
因而g(x)∈[g(![]() ),+∞),不符合题意.
),+∞),不符合题意.
综上,-4-4ln 2≤a<0.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|+lnx(其中a为常数)
(1)若a=0,求函数g(x)=![]() 的极值;
的极值;
(2)求函数f(x)的单调区间;
(3)令F(x)=f(x)-![]() ,当a≥2时,判断函数F(x)在(0,1]上零点的个数,并说明理由.
,当a≥2时,判断函数F(x)在(0,1]上零点的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某名校从![]() 年到
年到![]() 年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将
年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将![]() 年编号为
年编号为![]() ,
,![]() 年编为
年编为![]() ,以此类推……)
,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)将这![]() 年的数据分为人数不少于
年的数据分为人数不少于![]() 人和少于
人和少于![]() 人两组,按分层抽样抽取
人两组,按分层抽样抽取![]() 年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这
年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这![]() 年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于
年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于![]() 的概率是多少?;
的概率是多少?;
(2)根据最近![]() 年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测
年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测![]() 年该校考入清华、北大的人数。(结果要求四舍五入至个位)
年该校考入清华、北大的人数。(结果要求四舍五入至个位)
参考公式: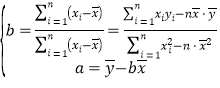
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米,最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米时,视角θ最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直, ![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 内部一点,点
内部一点,点![]() 在
在![]() 的延长线上,且PA=PB.
的延长线上,且PA=PB.
(Ⅰ)证明:OA=OB;
(Ⅱ)证明:平面PAB平面POC.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标有“甲”的袋中有![]() 个红球和
个红球和![]() 个白球,这些球除颜色外完全相同.
个白球,这些球除颜色外完全相同.
(Ⅰ)若从袋中依次取出![]() 个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
(Ⅱ)现从甲袋中取出个![]() 红球,
红球, ![]() 个白球,装入标有“乙”的空袋.若从甲袋中任取
个白球,装入标有“乙”的空袋.若从甲袋中任取![]() 球,乙袋中任取
球,乙袋中任取![]() 球,记取出的红球的个数为
球,记取出的红球的个数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,三点
,三点 中恰有二点在椭圆
中恰有二点在椭圆![]() 上,且离心率为
上,且离心率为![]() 。
。

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为椭圆
为椭圆![]() 的左右顶点,
的左右顶点, ![]() 为
为![]() 中点,求证:直线
中点,求证:直线![]() 与直线
与直线![]() 它们的斜率之积为定值;
它们的斜率之积为定值;
(3)若椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 斜率之和为定值。
斜率之和为定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com