
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.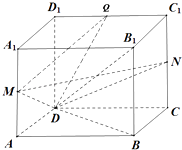
(1)求证:直线MN⊥平面B1BD;
(2)已知AA1=AB,AA1⊥AB,取线段C1D1的中点Q,求二面角Q﹣MD﹣N的余弦值.
【答案】
(1)
证明:∵四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,
∵M、N分别为棱AA1、CC1的中点,
∴MN∥AC,
∵在正方形ABCD中,AC⊥BD,
∴MN⊥BD,
∵BB1⊥AC,
∴MN⊥BB1,
∵BB1∩BD=B,
∴MN⊥平面BB1D
(2)
证明:∵AA1⊥AB,
∴四棱柱ABCD﹣A1B1C1D1为正方体,
以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,如图建立直角坐标系,
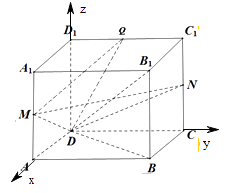
设棱长为2,
则M(2,0,1),D(0,0,0),N(0,2,1),Q(0,1,2),
易求得面MDN的一个法向量为 ![]() ,
,
则面QMD的一个法向量为 ![]() ,
,
则 ![]() ,
,
所以二面角Q﹣MD﹣N的余弦值为 ![]()
【解析】(1)根据线面垂直的判定定理即可证明.(2)建立空间坐标系,求出平面的法向量,利用向量法进行求解即可.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:点
,证明:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升”。其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升”,在该问题中第3天共分发大米( )
A. 192升 B. 213升 C. 234升 D. 255升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=ntm=n”类比得到“c≠0,a·c=b·ca=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“![]() ”类比得到
”类比得到![]() .以上的式子中,类比得到的结论正确的是________.
.以上的式子中,类比得到的结论正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.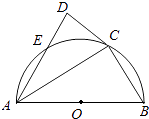
(1)求证:AC平分∠BAD;
(2)求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O为△ABC的外接圆,过点C作圆O的切线交AB的延长线于点D,∠ADC的平分线交AC于点E,∠ACB的平分线交AD于点H. 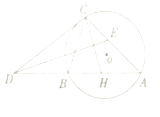
(1)求证:CH⊥DE;
(2)若AE=2CE.证明:DC=2DB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com