
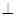 BQ并说明理由.
BQ并说明理由.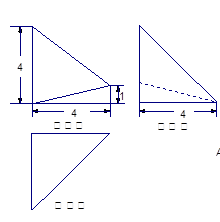
 ;(2)
;(2) ;(3)存在点Q,使得AQ
;(3)存在点Q,使得AQ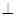 BQ.
BQ. BQ;法2:建立空间直角坐标系,转化为两对应向量数量积为零,求出点Q的坐标.
BQ;法2:建立空间直角坐标系,转化为两对应向量数量积为零,求出点Q的坐标. 面
面 ,且EC="BC=AC=4" ,BD=1,
,且EC="BC=AC=4" ,BD=1,

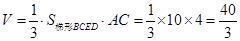 .
. . 3分
. 3分 ,BF=AF=
,BF=AF= .
.
 .
. . 7分
. 7分
 ,∴
,∴
 .
.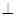 BQ. 8分
BQ. 8分
 ∴
∴ ∽
∽

 ∴
∴
 . 11分
. 11分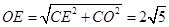 ,
,



 面
面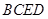 ,
, 面
面 ∴
∴ ∴
∴ 面
面 13分
13分 面ACQ
面ACQ . 14分
. 14分
 ,
,
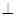 BQ ∴
BQ ∴ ①
①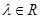
 使得
使得

 ②
② ,解得
,解得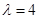
 .
.

科目:高中数学 来源:不详 题型:单选题
 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )A.2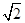 | B.2 | C.4 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com