已知函数f(x)=mx3+nx2(m,n∈R,m≠0),函数y=f(x)的图象在点(2,f(2))处切线与x轴平行,
(1)用关于m的代数式表示n;
(2)求函数f(x)的单调递增区间;
(3)若x1>2,记函数y=f(x)的图象在点M(x1,f(x1))处的切线l与x轴的交点为(x2,0),证明:x2≥3.
解:(1)∵f(x)=m
3x+nx
2,
∴f′(x)=3mx
2+2nx.
由题意得:f′(2)=0,即3m+n=0,
∴n=-3m;(4分)
(2)∵n=-3m,
∴f(x)=mx
3-3mx
2,f′(x)=3mx
2-6mx,
令f′(x)>0,
得3mx
2-6mx>0,
当m>0时,∴x<0或x>2,
∴函数f(x)的单调递增区间为(-∞,0),(2,+∞),
当m<0时,函数f(x)的单调递增区间为(0,2);(8分)
(3)由(1)得:f(x)=mx
3-3mx
2,f′(x)=3mx
2-6mx,
l:y-(mx
13-3mx
12)=(3mx
12-6mx
1)(x-x
1),
令y=0,由m≠0,x
1>2,则

,
所以
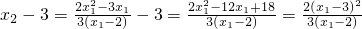
,
∵x
1>2.(x
1-3)
2≥0,
∴x
2-3≥0,即x
2≥3.(12分)
分析:(1)由f(x)的解析式,求出f(x)的导函数,由切线与x轴平行,得到切线斜率为0,故把x=2代入导函数求出的导函数值为0,列出关于m与n的关系式,用关于m的代数式表示出n即可;
(2)把(1)表示出的n代入f(x)和导函数中,令导函数大于0,分m大于0和小于0两种情况考虑,分别求出不等式的解集即可得到函数的单调递增区间;
(3)把x=x
1代入(1)求出的导函数,表示出切线l的斜率,代入f(x)求出切点的纵坐标,确定出切点坐标,根据切点坐标和斜率写出切线l的方程,然后令y=0表示出x
2,利用作差法,根据x
1>2,及完全平方式大于等于0得到x
2-3大于等于0,变形即可得证.
点评:此题考查了利用导数研究曲线上某点的切线方程,以及利用导数研究函数的单调性.要求学生掌握切点横坐标对应的导函数值为切线方程的斜率,导函数值大于0时x的范围为函数的递增区间,导函数值小于0时x的范围为函数的递减区间,熟练运用这些性质是解本题的关键.

 ,
,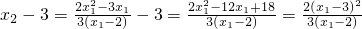 ,
,

 考前必练系列答案
考前必练系列答案