
【题目】如果函数![]() 满足
满足![]() 且
且![]() 是它的零点,则函数
是它的零点,则函数![]() 是“有趣的”,例如
是“有趣的”,例如![]() 就是“有趣的”,已知
就是“有趣的”,已知![]() 是“有趣的”.
是“有趣的”.
(1)求出b、c并求出函数![]() 的单调区间;
的单调区间;
(2)若对于任意正数x,都有![]() 恒成立,求参数k的取值范围.
恒成立,求参数k的取值范围.
【答案】(1)![]() ,
,![]() ,单减区间为0,1),单增区间为
,单减区间为0,1),单增区间为![]() ;(2)
;(2)![]()
【解析】
(1)根据定义得方程恒成立,解得b、c,再根据复合函数单调性确定函数![]() 的单调区间;
的单调区间;
(2)先化简不等式,再求导数,根据导函数符号分类讨论,利用导数证明![]() 恒成立,再说明
恒成立,再说明![]() 不恒成立.
不恒成立.
(1)因为![]() 是“有趣的”,所以
是“有趣的”,所以![]()
即![]()
![]()
![]()
![]() 的定义域为
的定义域为![]() ,单减区间为(0,1),单增区间为
,单减区间为(0,1),单增区间为![]() .
.
(2)参数![]() 的取值范围为
的取值范围为![]() .
.
引理:不等式![]() 对任意正数y都成立。证明如下:
对任意正数y都成立。证明如下:
![]()
由![]() 恒成立,得
恒成立,得![]() 恒成立。.
恒成立。.
我们构造函数![]() 。注意到
。注意到![]() 。
。

构造![]() ,注意到
,注意到![]() ,且
,且
![]()
我们以下分两部分进行说明:
第一部分:![]() 时,
时,![]() 恒成立。
恒成立。
![]() 时,由引理得:
时,由引理得:![]() ,知道
,知道![]() ,
,
从而当![]() 时有
时有![]() ,
,![]() 时有
时有![]() ,所以
,所以 在(0,1)上为负,在
在(0,1)上为负,在![]() 上为正。
上为正。
从而![]() 在
在![]() 上单减,在
上单减,在![]() 上单增,最小值为
上单增,最小值为![]() 。
。
从而![]()
第二部分:![]() 时,不满足条件。
时,不满足条件。
构造函数![]() 。
。
(ⅰ)若![]() ,则对于任意
,则对于任意![]() ,都有
,都有![]() 。
。
(ⅱ)若![]() ,则对于任意
,则对于任意![]() ,
,![]() ,
,
而 ,所以在(0,1)上
,所以在(0,1)上![]() 有唯一零点
有唯一零点![]() ,同时在
,同时在![]() ,时都有
,时都有![]() 。
。
于是只要![]() ,无论是(ⅰ)还是(ⅱ),我们总能找到一个实数
,无论是(ⅰ)还是(ⅱ),我们总能找到一个实数![]() ,在
,在![]() 时都有
时都有![]() 。
。
这样在 时,都有
时,都有![]() ,结合
,结合![]() ,所以
,所以 时
时![]() ,从而在
,从而在 时有
时有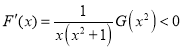 。
。![]() ,所以
,所以 时
时![]() ,不满足要求。
,不满足要求。


科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() ;
;
(2)若从![]() 中抽取一个公比为
中抽取一个公比为![]() 的等比数列
的等比数列![]() ,其中
,其中![]() ,且
,且![]() ,
,
(i)求![]() 的通项公式;
的通项公式;
(ii)记数列的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 满足的条件;若不存在,请说明理由.
满足的条件;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等腰梯形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]()
![]() ,将
,将![]() 沿着
沿着![]() 翻折成
翻折成![]() ,使平面
,使平面![]() 平面
平面![]() .
.


(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在点P,使得
上是否存在点P,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用极坐标与直角坐标的互化公式可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
,消去参数![]() 可知曲线
可知曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,由直线
的圆,由直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得: ![]() ;则曲线C的方程为
;则曲线C的方程为![]() , 再次利用极坐标与直角坐标的互化公式可得
, 再次利用极坐标与直角坐标的互化公式可得
可得曲线C的极坐标方程.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面积的最大值.
面积的最大值.
试题解析:(1)由题意可知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,直线
的圆,直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得:  ;可知曲线C的方程为
;可知曲线C的方程为![]() ,
,
所以曲线C的极坐标方程为![]() ,
,
即![]() .
.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
当![]() 时,
时, ![]() ,
,
所以△MON面积的最大值为![]() .
.
【题型】解答题
【结束】
23
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.若曲线
轴正半轴为极轴建立极坐标系.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 点的极坐标为
点的极坐标为![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程以及点
的直角坐标方程以及点![]() 的直角坐标;
的直角坐标;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际羽毛球比赛规则从2006年5月开始,正式决定实行21分的比赛规则和每球得分制,并且每次得分者发球,所有单项的每局获胜分至少是21分,最高不超过30分,即先到21分的获胜一方赢得该局比赛,如果双方比分为![]() 时,获胜的一方需超过对方2分才算取胜,直至双方比分打成
时,获胜的一方需超过对方2分才算取胜,直至双方比分打成![]() 时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为
时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为![]() ,甲接发球贏球的概率为
,甲接发球贏球的概率为![]() ,则在比分为
,则在比分为![]() ,且甲发球的情况下,甲以
,且甲发球的情况下,甲以![]() 赢下比赛的概率为( )
赢下比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2019这2019个数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列![]() ,则此数列的项数为( )
,则此数列的项数为( )
A.167B.168C.169D.170
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆C1和抛物线C2有相同的焦点(1,0),椭圆C1过点![]() ,抛物线
,抛物线![]() 的顶点为原点.
的顶点为原点.
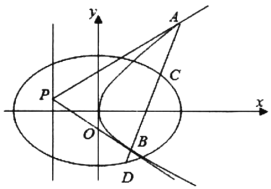
(1)求椭圆C1和抛物线C2的方程;
(2)设点P为抛物线C2准线上的任意一点,过点P作抛物线C2的两条切线PA,PB,其中A、B为切点.
设直线PA,PB的斜率分别为k1,k2,求证:k1k2为定值;
②若直线AB交椭圆C1于C,D两点,S△PAB,S△PCD分别是△PAB,△PCD的面积,试问:![]() 是否有最小值?若有,求出最小值;若没有,请说明理由.
是否有最小值?若有,求出最小值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com