
【题目】成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在![]() 评定为“优”,奖励3面小红旗;得分在
评定为“优”,奖励3面小红旗;得分在![]() 评定为“良”,奖励2面小红旗;得分在
评定为“良”,奖励2面小红旗;得分在![]() 评定为“中”,奖励1面小红旗;得分在
评定为“中”,奖励1面小红旗;得分在![]() 评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如下图:
评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如下图:
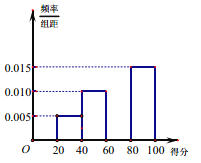
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“优”、“良”、“中”、“差”的班级中抽取10个班级,再从这10个班级中随机抽取2个班级进行抽样复核,记抽样复核的2个班级获得的奖励小红旗面数和为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
【答案】(1)中位数为70分.(2)见解析,![]()
【解析】
(1)根据频率分布直方图中中位数的计算公式计算即可.
(2)先根据分层抽样确定10个班级中优”、“良”、“中”、“差”的班级的人数,再根据奖励小红旗的面数确定![]() 的可能取值,再根据古典概型概率计算公式求解
的可能取值,再根据古典概型概率计算公式求解![]() 每个取值对应的概率,最后列出分布列求解数学期望.
每个取值对应的概率,最后列出分布列求解数学期望.
解:(1)得分![]() 的频率为
的频率为![]() ;
;
得分![]() 的频率为
的频率为![]() ;
;
得分![]() 的频率为
的频率为![]() ;
;
所以得分![]() 的频率为
的频率为![]() .
.
设班级得分的中位数为![]() 分,于是
分,于是![]() ,解得
,解得![]() .
.
所以班级卫生量化打分检查得分的中位数为70分.
(2)由(1)知题意“优”、“良”、“中”、“差”的频率分别为0.3,0.4,0.2,0.1.又班级总数为40.于是“优”、“良”、“中”、“差”的班级个数分别为12,16,8,4.
分层抽样的方法抽取的“优”、“良”、“中”、“差”的班级个数分别为3,4,2,1.
由题意可得![]() 的所有可能取值为1,2,3,4,5,6.
的所有可能取值为1,2,3,4,5,6.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
![]() .
.
所以![]() 的数学期望
的数学期望![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂A,B两条生产线生产同款产品,若该产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从A,B生产线的产品中各随机抽取100件进行检测,结果统计如下图:
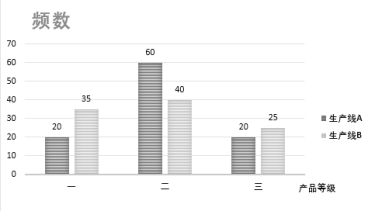
(I)根据已知数据,判断是否有![]() 的把握认为一等级产品与生产线有关?
的把握认为一等级产品与生产线有关?
(II)求抽取的200件产品的平均利润;
(III)估计该厂若产量为2000件产品时,一等级产品的利润.
附:独立性检验临界值表
|
|
|
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
|
|
|
| … |
(参考公式: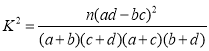 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上的一点,其焦点为点
上的一点,其焦点为点![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线
处的切线![]() 交圆
交圆![]() :
:![]() 于不同的两点
于不同的两点![]() ,
,![]() .
.
(1)若点![]() ,求
,求![]() 的值;
的值;
(2)设点![]() 为弦
为弦![]() 的中点,焦点
的中点,焦点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上靠近
上靠近![]() 的三等分点.现沿
的三等分点.现沿![]() 进行翻折,得到四棱锥
进行翻折,得到四棱锥![]() ,如图2,且
,如图2,且![]() .在图2中:
.在图2中:
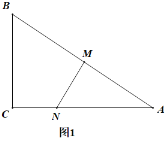

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉市掀起了轰轰烈烈的“十日大会战”,要在10天之内,对武汉市民做一次全员检测,彻底摸清武汉市的详细情况.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方案①:将每个人的血分别化验,这时需要验1000次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验这样,该组
个人的血样再分别进行一次化验这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次. 假设此次检验中每个人的血样化验呈阳性的概率为
次. 假设此次检验中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() . 试比较方案②中,
. 试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com