
【题目】2019年1月1日起我国实施了个人所得税的新政策,新政策的主要内容有:①个税起征点为5000元,②每月应纳税所得额(含税)=收入![]() 个税起征点
个税起征点![]() 专项附加扣除.赵先生某月收入
专项附加扣除.赵先生某月收入![]() 元,符合赡养老人与子女教育专项附加扣除,共计3000元.
元,符合赡养老人与子女教育专项附加扣除,共计3000元.
新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | … |
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元25000元的部分 | … |
税率(%) | 3 | 10 | 20 | … |
(1)当![]() 时,赵先生当月应缴纳的个税额是多少?
时,赵先生当月应缴纳的个税额是多少?
(2)设赵先生当月应缴纳的个税额是![]() 元,若
元,若![]() ,请求出
,请求出![]() 关于
关于![]() 的函数;
的函数;
(3)若赵先生该月应纳的个税额为3020元,问他的月收入![]() 是多少元?
是多少元?
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位开展岗前培训期间,甲、乙2人参加了5次考试,成绩统计如下:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩 | 82 | 82 | 79 | 95 | 87 |
乙的成绩 | 95 | 75 | 80 | 90 | 85 |
(1)根据有关统计知识回答问题:若从甲、乙2人中选出1人上岗,你认为选谁合适?请说明理由;
(2)根据有关概率知识解答以下问题:若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油![]() 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(2,0),动点P满足:点P到直线x=-1的距离比其到点F的距离小1.
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过F作直线l垂直于x轴与曲线C交于A、B两点,Q是曲线C上异于A、B的一点,设曲线C在点A、B、Q处的切线分别为l1、l2、l3,切线l1、l2交于点R,切线l1、l3交于点S,切线l2、l3交于点T,若![]() RST的面积为6,求Q点的横坐标.
RST的面积为6,求Q点的横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手车直卖网站对其所经营的一款品牌汽车的使用年数x与销售价格y(单位:万元,辆)进行了记录整理,得到如下数据:

(I)画散点图可以看出,z与x有很强的线性相关关系,请求出z与x的线性回归方程(回归系数![]() 精确到0.01);
精确到0.01);
(II)求y关于x的回归方程,并预测某辆该款汽车当使用年数为10年时售价约为多少.
参考公式:
参考数据: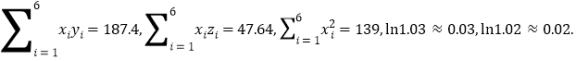
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com