【题目】下列说法：
①分类变量
与
的随机变量
越大，说明“
与
有关系”的可信度越大.
②以模型
去拟合一组数据时，为了求出回归方程，设
，将其变换后得到线性方程
，则
的值分别是
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
中， 
，
则
.正确的个数是（ ）
A. 0 B. 1 C. 2 D. 3
科目：高中数学 来源： 题型：
【题目】给出下列四个结论：
（1）如果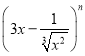
的展开式中各项系数之和为128，则展开式中
的系数是-21；
（2）用相关指数
来刻画回归效果， 
的值越大，说明模型的拟合效果越差；
（3）若
是
上的奇函数，且满足
，则
的图象关于
对称；
（4）一个篮球运动员投篮一次得3分的概率为
，得2分的概率为
，不得分的概率为
，且
，已知他投篮一次得分的数学期望为2，则
的最小值为
；
其中正确结论的序号为__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某医药研究所开发一种新药，在试验药效时发现：如果成人按规定剂量服用，那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y＝
其对应曲线(如图所示)过点
.
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值)；
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效，那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为确立下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量
（单位： 
）和年利润
（单位：千元）的影响.对近
年的宣传费
和年销售量
数据作了初步处理，得到下面的散点图及一些统计量的值.
表中
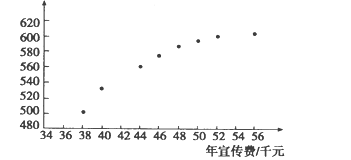
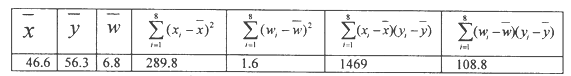
（Ⅰ）根据散点图判断， 
与
哪一个适宜作为年销售量
关于年宣传费
的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立
关于
的回归方程；
（Ⅲ）已知这种产品的年利率
与
的关系为
.根据（Ⅱ）的结果回答下列问题：
（i）年宣传费
时，年销售量及利润的预报值是多少？
（ii）年宣传费
为何值时，年利率的预报值最大？
附：对于一组数据
……
，其回归线
的斜率和截距的最小二乘法估计分别为： 
， 
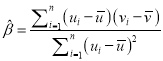查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x2＋bx为偶函数，数列{an}满足an＋1＝2f(an－1)＋1，且a1＝3，an>1.
(1)设bn＝log2(an－1)，证明：数列{bn＋1}为等比数列；
(2)设cn＝nbn，求数列{cn}的前n项和Sn.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分14分）
已知函数
（
为常数）的图像与
轴交于点
，曲线
在点
处的切线斜率为
.
（1）求
的值及函数
的极值；
（2）证明：当
时，
（3）证明：对任意给定的正数
，总存在
，使得当
时，恒有
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数f(x)，若存在x0∈R，使得f(x0)=x0成立，则称x0为f(x)的天宫一号点.已知函数f(x)=ax2+(b-7)x+18的两个天宫一号点分别是-3和2.
(1)求a,b的值及f(x)的表达式；
(2)当函数f(x)的定义域是［t,t+1］时，求函数f(x)的最大值g(t).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f(x)的定义域为(－3,3)，
满足f(－x)＝－f(x)，且对任意x，y，都有f(x)－f(y)＝f(x－y)，当x<0时，f(x)>0，f(1)＝－2.
(1)求f(2)的值；
(2)判断f(x)的单调性，并证明；
(3)若函数g(x)＝f(x－1)＋f(3－2x)，求不等式g(x)≤0的解集．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
