
分析 (1)由题意可得-2,0为方程f(x)=0的两个实根,代入f(x),解方程可得b,c的值,进而得到f(x)的解析式;
(2)求出g(x)的对称轴,讨论与区间(2,3)的关系,即可得到所求m的范围;
(3)依题得,n≤3-f(x)=-3x2-6x+3对于任意的x∈[-2,2]恒成立,只要n≤(-3x2-6x+3)min,x∈[-2,2],由单调性可得最小值,即可得到n的范围.
解答 解:(1)依题得,-2,0为方程f(x)=0的两个实根,
即有$\left\{\begin{array}{l}{f(-2)=0}\\{f(0)=0}\end{array}\right.$即$\left\{\begin{array}{l}{12-2b+c=0}\\{c=0}\end{array}\right.$,
解得b=6,c=0.
则f(x)=3x2+6x;
(2)函数g(x)=f(x)+mx-2=3x2+(m+6)x-2在(2,3)上单调,
又二次函数开口向上,对称轴x=-$\frac{m+6}{6}$,
即有-$\frac{m+6}{6}$≤2或-$\frac{m+6}{6}$≥3,
解得m≥-18或m≤-24;
(3)依题得,n≤3-f(x)=-3x2-6x+3对于任意的x∈[-2,2]恒成立,
只要n≤(-3x2-6x+3)min,x∈[-2,2],
设h(x)=-3x2-6x+3,x∈[-2,2],
当x=2时,h(x)min=-21,
即有n≤-21.
点评 本题考查二次函数和二次方程及二次不等式的关系,考查单调性的运用,以及不等式恒成立问题的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2一$\sqrt{21}$i | B. | $\sqrt{21}$一2i | C. | 1一2i | D. | 2一i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
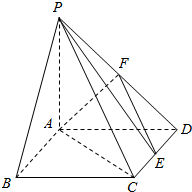 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2-2$|\begin{array}{l}{x}\end{array}|$
已知函数f(x)=x2-2$|\begin{array}{l}{x}\end{array}|$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com