
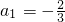 ,满足
,满足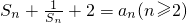 ,计算S1,S2,S3,S4,并猜想Sn的表达式.
,计算S1,S2,S3,S4,并猜想Sn的表达式. ,
, =an-2(n≥2,n∈N),令n=2可得
=an-2(n≥2,n∈N),令n=2可得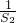 =a2-2=S2-a1-2,
=a2-2=S2-a1-2,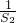 =
= -2,
-2, .
. ,S4=-
,S4=- .
. ,n∈N+,下边用数学归纳法证明:
,n∈N+,下边用数学归纳法证明: ,猜想成立.
,猜想成立.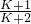 ,则当n=k+1时,∵Sn+
,则当n=k+1时,∵Sn+ =an-2,∴
=an-2,∴ ,
, ,∴
,∴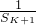 =
=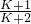 -2=
-2=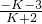 ,
,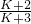 ,∴当n=k+1时,猜想仍然成立.
,∴当n=k+1时,猜想仍然成立. ,n∈N+成立.
,n∈N+成立. ,n∈N+;用数学归纳法证明,检验n=1时,猜想成立;假设SK=-
,n∈N+;用数学归纳法证明,检验n=1时,猜想成立;假设SK=-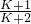 ,则当n=k+1时,由条件可得,
,则当n=k+1时,由条件可得, ,解出 SK+1=-
,解出 SK+1=-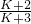 ,故n=k+1时,猜想仍然成立.
,故n=k+1时,猜想仍然成立. ,n∈N+,是解题的难点.
,n∈N+,是解题的难点. 

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com