
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为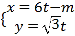 (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 上的动点
上的动点![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
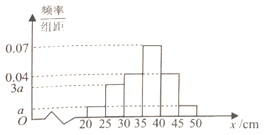
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:![]() ).经统计,高度在区间
).经统计,高度在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图,其中高度不低于
分成6组,制成如图所示的频率分布直方图,其中高度不低于![]() 的树苗为优质树苗.
的树苗为优质树苗.
附:
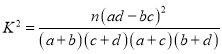 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
(1)求频率分布直方图中![]() 的值;
的值;
(2)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下![]() 列联表所示,将列联表补充完整,并根据列联表判断是否有
列联表所示,将列联表补充完整,并根据列联表判断是否有![]() %的把握认为优质树苗与地区有关?
%的把握认为优质树苗与地区有关?
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车是碳排放量比较大的行业之一,欧盟规定,从2015年开始,将对![]() 排放量超过130g/km的
排放量超过130g/km的![]() 型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类
型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类![]() 型品牌抽取5辆进行
型品牌抽取5辆进行![]() 排放量检测,记录如下(单位:g/km):
排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | y | 160 |
经测算发现,乙品牌车![]() 排放量的平均值为
排放量的平均值为![]() .
.
(Ⅰ)从被检测的5辆甲类品牌中任取2辆,则至少有一辆![]() 排放量超标的概率是多少?
排放量超标的概率是多少?
(Ⅱ)若乙类品牌的车比甲类品牌的![]() 的排放量的稳定性要好,求x的范围.
的排放量的稳定性要好,求x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若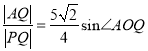 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有橡皮泥制作的底面半径为5,高为9的圆锥和底面半径为![]() ,高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为_________;若新圆锥的内接正三棱柱表面积取到最大值,则此正三棱柱的底面边长为_________.
,高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为_________;若新圆锥的内接正三棱柱表面积取到最大值,则此正三棱柱的底面边长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com