
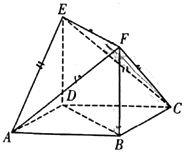
【题目】如图所示的多面体中,![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面 ![]() ;
;
(2)在线段![]() 上取一点
上取一点![]() ,当二面角
,当二面角![]() 的大小为
的大小为![]() 时,求
时,求![]() .
.
【答案】(1)见证明;(2) ![]()
【解析】
(1)取AE的中点M,先证明∠AMC就是二面角A-EF-C的平面角,再证明![]() ,即证平面
,即证平面![]() 平面
平面 ![]() ;(2)以AC与BD交点O为坐标原点,0A、OB分别为
;(2)以AC与BD交点O为坐标原点,0A、OB分别为![]() 轴建立直角坐标系,设
轴建立直角坐标系,设![]() ,利用向量法求得
,利用向量法求得![]() ,解方程即得
,解方程即得![]() .
.
解:(1)取AE的中点M.由于ED⊥面ABCD,ED//FB,
∴DE⊥AD,ED⊥DC,FB⊥BC,FB⊥AB,又ABCD是菱形,BDEF是矩形,
所以△ADE,△CDE,△ABF,△CBF是全等直角三角形,AE=AF,CE=CF,
所以AM⊥EF,CM⊥EF,∠AMC就是二面角A-EF-C的平面角
经计算![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
所以平面AEF⊥平面CEF.
(2)以AC与BD交点O为坐标原点,0A、OB分别为![]() 轴建立直角坐标系,由AD=BD=2,则A(
轴建立直角坐标系,由AD=BD=2,则A(![]() ,0,0),M(0,O,
,0,0),M(0,O,![]() ),C(﹣
),C(﹣![]() ,0,0),E(0,﹣1,
,0,0),E(0,﹣1,![]() ),
),
F(0,1,![]() ),
),![]() .
.
平面CEF的一个法向量![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,![]()
设平面NEF的法向量![]() ,则
,则
得![]() ,
,
令![]() ,则
,则![]() ,得
,得![]() .
.
因为二面角![]() 的大小为60°,
的大小为60°,
所以![]() ,
,
![]() 整理得
整理得![]() ,解得
,解得![]()
所以![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
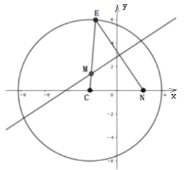
【题目】已知点![]() ,在圆
,在圆![]() :
:![]() 上任取一点
上任取一点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .(如图).
.(如图).
(1)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若过点![]() 的动直线
的动直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点.问:平面内是否存在异于点
两点.问:平面内是否存在异于点![]() 的定点
的定点![]() ,使得
,使得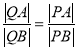 恒成立?试证明你的结论.
恒成立?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(2,-1),和直线x+y=1相切,且圆心在直线y=-2x上.
(1)求圆C的方程;
(2)已知直线l经过(2,0)点,并且被圆C截得的弦长为2,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列推理不属于合情推理的是( )
A. 由铜、铁、铝、金、银等金属能导电,得出一切金属都能导电.
B. 半径为![]() 的圆面积
的圆面积![]() ,则单位圆面积为
,则单位圆面积为![]() .
.
C. 由平面三角形的性质推测空间三棱锥的性质.
D. 猜想数列2,4,8,…的通项公式为![]() .
. ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .下列命题正确的为_______________.
.下列命题正确的为_______________.

①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西安市自2017年5月启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,斑马线前礼让行人也成为了一张新的西安“名片”.
但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患及机动车通畅率降低,交警部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到![]() 列联表如下:
列联表如下:
30岁以下 | 30岁以上 | 合计 | |
闯红灯 | 60 | ||
未闯红灯 | 80 | ||
合计 | 200 |
近期,为了整顿“行人闯红灯”这一不文明及项违法行为,交警部门在该十字路口试行了对闯红灯行人进行经济处罚,并从试行经济处罚后穿越该路口行人中随机抽取了200人进行调查,得到下表:
处罚金额 | 5 | 10 | 15 | 20 |
闯红灯的人数 | 50 | 40 | 20 | 0 |
将统计数据所得频率代替概率,完成下列问题.
(Ⅰ)将![]() 列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
(Ⅱ)当处罚金额为10元时,行人闯红灯的概率会比不进行处罚降低多少;
(Ⅲ)结合调查结果,谈谈如何治理行人闯红灯现象.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.132 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ,过
,过![]() 作动直线
作动直线![]() 交抛物线于
交抛物线于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() .
.
(1)若![]() 与
与![]() 重合,求直线
重合,求直线![]() 的方程;
的方程;
(2)求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com