
【题目】已知函数f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范围.
【答案】(Ⅰ)答案见解析(Ⅱ)![]()
【解析】
试题(Ⅰ)f′(x)=a﹣ex,x∈R.对a分类讨论,利用导数研究函数的单调性即可得出;
(Ⅱ)由x0∈(0,+∞),使不等式f(x)≤g(x)﹣ex,即a≤![]() .设h(x)=
.设h(x)=![]() ,则问题转化为a
,则问题转化为a![]() ,利用导数研究函数的单调性极值与最值即可得出.
,利用导数研究函数的单调性极值与最值即可得出.
解:(Ⅰ)∵f′(x)=a﹣ex,x∈R.
当a≤0时,f′(x)<0,f(x)在R上单调递减;
当a>0时,令f′(x)=0得x=lna.
由f′(x)>0得f(x)的单调递增区间为(﹣∞,lna);
由f′(x)<0得f(x)的单调递减区间为(lna,+∞).
(Ⅱ)∵x0∈(0,+∞),使不等式f(x)≤g(x)﹣ex,则![]() ,即a≤
,即a≤![]() .
.
设h(x)=![]() ,则问题转化为a
,则问题转化为a![]() ,
,
由h′(x)=![]() ,令h′(x)=0,则x=
,令h′(x)=0,则x=![]() .
.
当x在区间(0,+∞) 内变化时,h′(x)、h(x)变化情况如下表:

由上表可知,当x=![]() 时,函数h(x)有极大值,即最大值为
时,函数h(x)有极大值,即最大值为![]() .
.
∴![]() .
.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统 计,在2018年这一年内从![]() 市到
市到![]() 市乘坐高铁或飞机出行的成年人约为
市乘坐高铁或飞机出行的成年人约为![]() 万人次.为了 解乘客出行的满意度,现从中随机抽取
万人次.为了 解乘客出行的满意度,现从中随机抽取![]() 人次作为样本,得到下表(单位:人次):
人次作为样本,得到下表(单位:人次):
满意度 | 老年人 | 中年人 | 青年人 | |||
乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | |
10分(满意) | 12 | 1 | 20 | 2 | 20 | 1 |
5分(一般) | 2 | 3 | 6 | 2 | 4 | 9 |
0分(不满意) | 1 | 0 | 6 | 3 | 4 | 4 |
(span>1)在样本中任取![]() 个,求这个出行人恰好不是青年人的概率;
个,求这个出行人恰好不是青年人的概率;
(2)在2018年从![]() 市到
市到![]() 市乘坐高铁的所有成年人中,随机选取
市乘坐高铁的所有成年人中,随机选取![]() 人次,记其中老年人出行的人次为
人次,记其中老年人出行的人次为![]() .以频率作为概率,求
.以频率作为概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)如果甲将要从![]() 市出发到
市出发到![]() 市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于双曲线![]() ,定义
,定义![]() 为其伴随曲线,记双曲线
为其伴随曲线,记双曲线![]() 的左、右顶点为
的左、右顶点为![]() 、
、![]() .
.
(1)当![]() 时,记双曲线
时,记双曲线![]() 的半焦距为
的半焦距为![]() ,其伴随椭圆
,其伴随椭圆![]() 的半焦距为
的半焦距为![]() ,若
,若![]() ,求双曲线
,求双曲线![]() 的渐近线方程.
的渐近线方程.
(2)若双曲线![]() 的方程为
的方程为![]() ,弦
,弦![]() 轴,记直线
轴,记直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求其动点
,求其动点![]() 的轨迹方程.
的轨迹方程.
(3)过双曲线![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,求证:对任意的
两点,求证:对任意的![]() ,在伴随曲线
,在伴随曲线![]() 上总存在点
上总存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=6sinθ,建立以极点为坐标原点,极轴为x轴正半轴的平面直角坐标系.直线l的参数方程是![]() ,(t为参数).
,(t为参数).
(1)求曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点,且|AB|=![]() ,求直线的斜率k.
,求直线的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线,![]() 是两个不同的平面,则下列命题中正确命题的序号是( )
是两个不同的平面,则下列命题中正确命题的序号是( )
①若直线![]() 平行于平面
平行于平面![]() 内的无数条直线,则直线
内的无数条直线,则直线![]() ∥平面
∥平面![]() .
.
②若直线![]() ∥平面
∥平面![]() ,直线
,直线![]() ∥直线
∥直线![]() ,则直线
,则直线![]() 平行于平面
平行于平面![]() 内的无数条直线.
内的无数条直线.
③若直线![]() 不平行,则
不平行,则![]() 不可能垂直于同一平面.
不可能垂直于同一平面.
④若直线![]() ∥平面
∥平面![]() ,平面
,平面![]() 平面
平面![]() ,则直线
,则直线![]() 平面
平面![]()
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一名曰“堑堵”的几何体,已知 AE⊥底面BCFE , DF ∥ AE , DF = AE = 1, CE =![]() ,四边形ABCD 是正方形.
,四边形ABCD 是正方形.

(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑.判断四面体 EABC 是否为鳖臑,若是,写出其 每一个面的直角,并证明;若不是,请说明理由.
(2)求四面体 EABC 的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三实验班的60名学生期中考试的语文、数学成绩都在![]() 内,其中语文成绩分组区间是:
内,其中语文成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数
.其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
| |
24 | 3 | ||||
数学人数 | 12 | 4 |
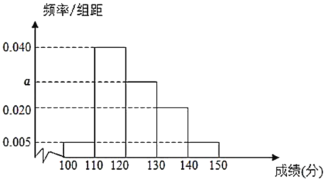
(1)求图中![]() 的值及数学成绩在
的值及数学成绩在![]() 的人数;
的人数;
(2)语文成绩在![]() 的3名学生均是女生,数学成绩在
的3名学生均是女生,数学成绩在![]() 的4名学生均是男生,现从这7名学生中随机选取4名学生,事件
的4名学生均是男生,现从这7名学生中随机选取4名学生,事件![]() 为:“其中男生人数不少于女生人数”,求事件
为:“其中男生人数不少于女生人数”,求事件![]() 发生的概率;
发生的概率;
(3)若从数学成绩在![]() 的学生中随机选取2名学生,且这2名学生中数学成绩在
的学生中随机选取2名学生,且这2名学生中数学成绩在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备投产一种新产品,经测算,已知每年生产![]() 万件的该种产品所需要的总成本
万件的该种产品所需要的总成本![]() (万元),依据产品尺寸,产品的品质可能出现优、中、差三种情况,随机抽取了1000件产品测量尺寸,尺寸分别在
(万元),依据产品尺寸,产品的品质可能出现优、中、差三种情况,随机抽取了1000件产品测量尺寸,尺寸分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:
(单位:![]() )中,经统计得到的频率分布直方图如图所示.
)中,经统计得到的频率分布直方图如图所示.
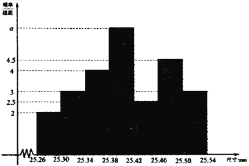
产品的品质情况和相应的价格![]() (元/件)与年产量
(元/件)与年产量![]() 之间的函数关系如下表所示.
之间的函数关系如下表所示.
产品品质 | 立品尺寸的范围 | 价格 |
优 |
|
|
中 |
|
|
差 |
|
|
以频率作为概率解决如下问题:
(1)求实数![]() 的值;
的值;
(2)当产量![]() 确定时,设不同品质的产品价格为随机变量
确定时,设不同品质的产品价格为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列;
的分布列;
(3)估计当年产量![]() 为何值时,该公司年利润最大,并求出最大值.
为何值时,该公司年利润最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com