
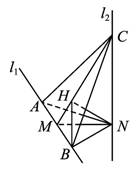
(Ⅰ)证明AC⊥NB;
(Ⅱ)若∠ACB=60°,求NB与平面ABC所成角的余弦值.
解法一:(Ⅰ)由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN,由已知MN⊥l1,AM=MB=MN,可知AN=NB且AN⊥NB,又AN为AC在平面ABN内的射影.
∴AC⊥NB.
(Ⅱ)∵Rt△CNA≌Rt△CNB.

∴AC=BC,又已知∠ACB=60°,因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB.
NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角.
在Rt△NHB中,cos∠NBH=![]() =
=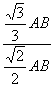 =
=![]() .
.
解法二:如图,建立空间直角坐标系M-xyz.令MN=1,则有A(-1,0,0),B(1,0,0),N(0,1,0).
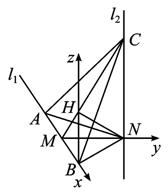
(Ⅰ)∵MN是l1,l2的公垂线,l2⊥l1.∴l2⊥平面ABN.∴l2平行于z轴.
故可设C(0,1,m),于是![]() =(1,1,m),
=(1,1,m),![]() =(1,-1,0).
=(1,-1,0).
∵![]() ·
·![]() =1+(-1)+0=0.
=1+(-1)+0=0.
∴AC⊥NB.
(Ⅱ)∵![]() =(1,1,m),
=(1,1,m), ![]() =(-1,1,m),
=(-1,1,m),
∴|![]() |=|
|=|![]() |.
|.
又已知∠ACB=60°,∴△ABC为正三角形,AC=BC=AB=2.
在Rt△CNB中,NB=![]() ,可得NC=
,可得NC=![]() ,故C(0,1,
,故C(0,1,![]() ).
).
连结MC,作MH⊥MC于H,设H(0,λ,![]() λ)(λ>0),
λ)(λ>0),
∴![]() =(0,1-λ,-
=(0,1-λ,-![]() λ),
λ),![]() =(0,1,
=(0,1,![]() ).
).
∵![]() ·
·![]() =1-λ-2λ=0,
=1-λ-2λ=0,
∴λ=![]() ,
,
H(0,![]() ,
,![]() ),可得
),可得![]() =(0,
=(0,![]() ,-
,-![]() ),连结BH,则
),连结BH,则![]() =(-1,
=(-1,![]() ,
,![]() ).
).
∴![]() ·
·![]() =0+
=0+![]() -
-![]() =0,∴
=0,∴![]() ⊥
⊥![]() ,又MC∩BH=H,
,又MC∩BH=H,
∴HN⊥平面ABC,∠NBH为NB与平面ABC所成的角.
又![]() =(-1,1,0),
=(-1,1,0),
cos∠NBH=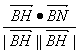 =
=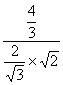 =
=![]() .
.


科目:高中数学 来源: 题型:
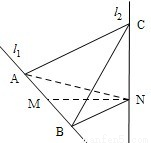
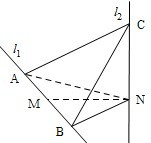 如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l1上,C在l2上,AM=MB=MN.
如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l1上,C在l2上,AM=MB=MN.查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题
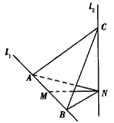
查看答案和解析>>
科目:高中数学 来源: 题型:
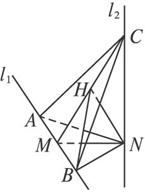
(1)证明AC⊥NB;
(2)若∠ACB=60°,求NB与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2006年全国统一高考数学试卷Ⅰ(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com