
【题目】(本小题满分为16分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为:
 ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
【答案】(1)不会获利,至少补贴5 000元(2)400
【解析】
试题分析:(1)解决实际问题关键为读懂题意:能否获利,决定于利润是否为正,故列出利润S函数关系式S=200x-![]() =-
=-![]() x2+400x-80 000=-
x2+400x-80 000=-![]() (x-400)2,当x∈[200,300]时,S<0,因此该单位不会获利,补贴的标准为S取得最大值-5 000,而不是最小值(2)先列出每吨的平均处理成本的函数关系式,为一个分段函数,需分段求最值,最后比较两段最小值的较小值为所求.
(x-400)2,当x∈[200,300]时,S<0,因此该单位不会获利,补贴的标准为S取得最大值-5 000,而不是最小值(2)先列出每吨的平均处理成本的函数关系式,为一个分段函数,需分段求最值,最后比较两段最小值的较小值为所求.
试题解析:(1)当x∈[200,300]时,设该项目获利为S,
则S=200x-![]() =-
=-![]() x2+400x-80 000=-
x2+400x-80 000=-![]() (x-400)2,
(x-400)2,
所以当x∈[200,300]时,S<0,因此该单位不会获利.
当x=300时,S取得最大值-5 000,
所以国家每月至少补贴5 000元才能使该项目不亏损.
(2)由题意可知二氧化碳的每吨处理成本为
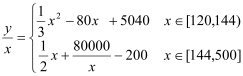
①当x∈[120,144)时,![]() =
=![]() x2-80x+5 040=
x2-80x+5 040=![]() (x-120)2+240,
(x-120)2+240,
所以当x=120时,![]() 取得最小值240.
取得最小值240.
②当x∈[144,500]时,![]() =
=![]() x+
x+![]() -200≥2
-200≥2![]() -200=200,
-200=200,
当且仅当![]() x=
x=![]() ,即x=400时,
,即x=400时,![]() 取得最小值200.因为200<240,
取得最小值200.因为200<240,
答:当每月的处理量为400吨时,才能使每吨的平均处理成本最低.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1= ![]() ,且对于任意正整数m,n都有an+m=anam . 若Sn<a对任意n∈N*恒成立,则实数a的最小值是 .
,且对于任意正整数m,n都有an+m=anam . 若Sn<a对任意n∈N*恒成立,则实数a的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,设命题p:函数f(x)=x2﹣2ax+1﹣2a在区间[0,1]上与x轴有两个不同的交点;命题q:g(x)=|x﹣a|﹣ax有最小值.若(¬p)∧q是真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记集合A={(x,y)|x2+y2≤16}和集合B={(x,y)|x+y﹣4≤0,x≥0,y≥0}表示的平面区域分别为Ω1 , Ω2 , 若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1)标签的选取是无放回的;
(2)标签的选取是有放回的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q≠1,则下面说法中不正确的是( )
A.{an+2+an}是等比数列
B.对于k∈N* , k>1,ak﹣1+ak+1≠2ak
C.对于n∈N* , 都有anan+2>0
D.若a2>a1 , 则对于任意n∈N* , 都有an+1>an
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(x1 , f(x1),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() .
.
(1)求函数f(x)的解析式;
(2)当x∈[0, ![]() ]时,求函数f(x)的单调递增区间;
]时,求函数f(x)的单调递增区间;
(3)当x∈[0, ![]() ]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com