分析:根据题意,分析选项,A、左边的不等式中的根号下的x-2大于0,而右边的不等式没有这个限制条件,所以两不等式不是同解不等式;
B、左边的不等式有x-1不为0的限制,而右边没有,所以两不等式不是同解不等式;
C、左边的不等式可化为(2x-3)(x-5)大于0,与右边的不等式完全相同,所以为同解不等式;
D、当2x-1小于0时,左边的不等式可化为x2-2x-6>2x-1,与右边的不等式不相同,所以不是同解不等式.
解答:解:A、由
(x2-4x+3)<0,可化为:
,由①得:x>2;由②得:1<x<3,
所以不等式的解集为:2<x<3;
而x
2-4x+3<0可化为:(x-1)(x-3)<0,解得:1<x<3,
所以两不等式不是同解不等式,此选项错误;
B、
≥0化为:
,由①得:x≥2或x≤1;由②得:x≠1,
所以不等式的解集为:x≥2或x<1;
而(x-1)(x-2)≥0,解得:x≥2或x≤1,所以两不等式不是同解不等式,此选项错误;
C、
>0可化为:(2x-3)(x-5)>0,解得x>5或x<
,所以两不等式为同解不等式,此选项正确;
D、
<1,移项合并得:
<0,
可化为:
或
或
,
解得:
<x<5;
而x
2-2x-6<2x-1,可化为:(x-5)(x+1)<0,解得:-1<x<5,
所以两不等式不是同解不等式,此选项错误,
所以正确的选项是C.
故选C
点评:此题考查了一元二次不等式的解法,考查了转化的数学思想,是一道综合题.



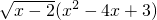 <0与x2-4x+3<0
<0与x2-4x+3<0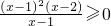 与(x-1)(x-2)≥0
与(x-1)(x-2)≥0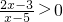 与(2x-3)(x-5)>0
与(2x-3)(x-5)>0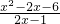 <1与x2-2x-6<2x-1
<1与x2-2x-6<2x-1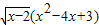 <0与x2-4x+3<0
<0与x2-4x+3<0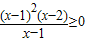 与(x-1)(x-2)≥0
与(x-1)(x-2)≥0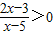 与(2x-3)(x-5)>0
与(2x-3)(x-5)>0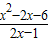 <1与x2-2x-6<2x-1
<1与x2-2x-6<2x-1