
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如表:
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R(公里) | ||
100≤R<180 | 180≤R<280 | <280 | |
纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
某校研究性学习小组,从汽车市场上随机选取了M辆纯电动乘用车,根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
分组 | 频数 | 频率 |
100≤R<180 | 3 | 0.3 |
180≤R<280 | 6 | x |
R≥280 | y | z |
合计 | M | 1 |
(1)求x、y、z、M的值;
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
【答案】
(1)解:由题意得: 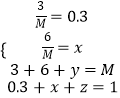 ,
,
解得x=0.6,y=1,z=0.1,M=10.
(2)解:从这M辆纯电动乘用车任选3辆,
基本事件总数n= ![]() =120,
=120,
10辆车中,有7辆车续驶里程不低于180公里,
选到的3辆车续驶里程都不低于180公里包含的基本事件个数m= ![]() =35,
=35,
∴选到的3辆车续驶里程都不低于180公里的概率p= ![]() =
= ![]() .
.
(3)解:由题意知X的可能取值为5,6.5,8,8.5,10,12,
P(X=5)=0.32=0.09,
P(X=6.5)= ![]() ,
,
P(X=8)=0.62=0.36,
P(X=8.5)= ![]() =0.06,
=0.06,
P(X=10)= ![]() ,
,
P(X=12)=0.12=0.01,
∴X的分布列为:
X | 5 | 6.5 | 8 | 8.5 | 10 | 12 |
P | 0.09 | 0.36 | 0.36 | 0.06 | 0.12 | 0.01 |
E(X)=5×0.09+6.5×0.36+8×0.36+8.5×0.06+10×0.12+12×0.01=7.5.
【解析】(1)由频率与频数的统计表列出方程组,能求出x、y、z、M的值.(2)从这M辆纯电动乘用车任选3辆,基本事件总数n= ![]() =120,10辆车中,有7辆车续驶里程不低于180公里,选到的3辆车续驶里程都不低于180公里包含的基本事件个数m=
=120,10辆车中,有7辆车续驶里程不低于180公里,选到的3辆车续驶里程都不低于180公里包含的基本事件个数m= ![]() =35,由此能求出选到的3辆车续驶里程都不低于180公里的概率.(3)由题意知X的可能取值为5,6.5,8,8.5,10,12,分别求出相应的概率,由此能求出X的分布列和E(X).
=35,由此能求出选到的3辆车续驶里程都不低于180公里的概率.(3)由题意知X的可能取值为5,6.5,8,8.5,10,12,分别求出相应的概率,由此能求出X的分布列和E(X).
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】小华与另外![]() 名同学进行“手心手背”游戏,规则是:
名同学进行“手心手背”游戏,规则是:![]() 人同时随机选择手心或手背其中一种手势,规定相同手势人数更多者每人得
人同时随机选择手心或手背其中一种手势,规定相同手势人数更多者每人得![]() 分,其余每人得
分,其余每人得![]() 分.现
分.现![]() 人共进行了
人共进行了![]() 次游戏,记小华
次游戏,记小华![]() 次游戏得分之和为
次游戏得分之和为![]() ,则
,则![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,AC=AA1=2,AB=BC=2 ![]() ,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D. 
(1)求证:BC1⊥平面AA1C1C;
(2)求二面角C1﹣AB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xOy中,过点P(﹣1,﹣2)的直线l的参数方程为 ![]() (t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsinθtanθ=2a(a>0),直线l与曲线C相交于不同的两点M、N.
(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsinθtanθ=2a(a>0),直线l与曲线C相交于不同的两点M、N.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|=|MN|,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=ax2+2x﹣lnx(a∈R).
(Ⅰ)若 a=4,求函数 f(x)的极值;
(Ⅱ)若 f′(x)在区间(0,1)内有唯一的零点 x0,求 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 f(x)=|x+2|﹣|x﹣3|﹣a
(Ⅰ)当 a=1 时,求函数 f(x)的最大值;
(Ⅱ)若 f(x)≤ ![]() 对任意 x∈R 恒成立,求实数 a 的取值范围.
对任意 x∈R 恒成立,求实数 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解端午节期间粽子的销售量,对其所在销售范围内的1000名消费者在端午节期间的粽子购买量(单位:g)进行了问卷调查,得到如图所示的频率分布直方图.

(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)求这1000名消费者的棕子购买量在600g~1400g的人数;
(Ⅲ)求这1000名消费者的人均粽子购买量(频率分布直方图中同一组的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三条直线型公路![]() ,
,![]() ,
,![]() 在点
在点![]() 处交汇,其中
处交汇,其中![]() 与
与![]() 、
、![]() 与
与![]() 的夹角都为
的夹角都为![]() ,在公路
,在公路![]() 上取一点
上取一点![]() ,且
,且![]() km,过
km,过![]() 铺设一直线型的管道
铺设一直线型的管道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(
上(![]() ,
,![]() 足够长),设
足够长),设![]() km,
km,![]() km.
km.
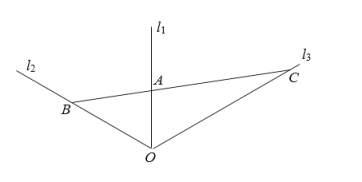
(1)求出![]() ,
,![]() 的关系式;
的关系式;
(2)试确定![]() ,
,![]() 的位置,使得公路
的位置,使得公路![]() 段与
段与![]() 段的长度之和最小.
段的长度之和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com