
����Ŀ��2013��������ȣ����ҵ��������Գ�������õ�Ʒѱ������������������õ�����������Ϊ���ࣺ��һ����õ������ڣ�0��170]���ڶ����ڣ�170��260]���������ڣ�260��+�ޣ�����λ��ǧ��ʱ����ijС������1000�������ֶ����ǵ��õ�������е��飬�õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��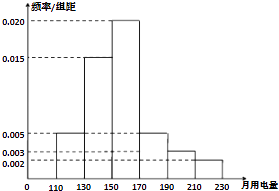
��1�����С�������õ�������λ����ƽ������
��2�����·ݸ�С��û�е�������õ继���֣�Ϊ���������Լ�õ磬���粿�ž������Ե�һ��ÿ������20ԪǮ���ڶ���ÿ������5ԪǮ����ÿ�������ý�����ƽ��ֵ��
��3�����÷ֲ�����ķ����Ӹ�С����ѡ��5λ������������Ӹ�5�������������ѡ���������������������õ��ʷ����ڲ�ͬ���͵ĸ��ʣ�
���𰸡�
��1���⣺��������һ�����ݵ�Ƶ��Ϊ0.004��20=0.08��
�ڶ������ݵ�Ƶ��Ϊ0.014��20=0.28��
���������ݵ�Ƶ��Ϊ0.020��20�T0.4��
����λ���ڵ����飬����λ��Ϊ150+x����0.08+0.28+0.020��x=0.5x=6��
����λ��Ϊ156��
ƽ����Ϊ120��0.1+140��0.3+160��0.4+180��0.1+200��0.06+220��0.04=156.8
��2���⣺��һ��ÿ����Ƶ��Ϊ0.1+0.3+0.4=0.8�����һ��ÿ������800����
�ڶ���ÿ����Ƶ��Ϊ0.1+0.06+0.04=0.2����ڶ���ÿ������200����
��ÿ�������ý�����ƽ��ֵΪ ![]() =17��Ԫ��
=17��Ԫ��
��3���⣺���÷ֲ�����ķ����Ӹ�С����ѡ��5λ������������ȡ����Ϊ ![]() =
= ![]() ��
��
���һ������ֱ�Ӧ��ȡ4����1����
��5�������������ѡ���������� ![]() =10��ѡ����
=10��ѡ����
���о����õ��ʷ����ڲ�ͬ������4��ѡ����
������õ��ʷ����ڲ�ͬ���͵ĸ���Ϊ ![]()
����������1��������λ���������ߵ�С�������֮���������λ�������ݸ���С���εױ��е�ĺ�������Զ�ӦС���ε����֮��Ϊ���ݵ�ƽ������ƽ��������2������Ƶ�ʷֲ�ֱ��ͼ��õ�һ������Ļ���������ÿ�������ý�����ƽ��ֵ����3�����ݷֲ�����ķ��������һ������ֱ�Ӧ��ȡ�Ļ���������������Ϸֱ�����5�������������ѡ��������;����õ��ʷ����ڲ�ͬ���͵�ѡ������������ŵ�����ʹ�ʽ���㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
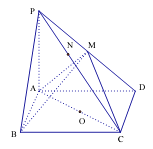
����Ŀ��������![]() �У�����
�У�����![]() �Ǿ��Σ�
�Ǿ��Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() ����
����![]() ���е�
���е�![]() Ϊ���ģ�
Ϊ���ģ� ![]() Ϊֱ�������潻
Ϊֱ�������潻![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .
.
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ������ԭ��ΪԲ�ģ���Բ�Ľ���Ϊֱ����Բ��ֱ��
������ԭ��ΪԲ�ģ���Բ�Ľ���Ϊֱ����Բ��ֱ��![]() ���У�
���У�![]() Ϊ������.
������.

��1������Բ![]() �ı����̣�
�ı����̣�
��2����ͼ������Բ��![]() ���ҽ���ֱ�Ϊ
���ҽ���ֱ�Ϊ![]() ����
����![]() ��ֱ��
��ֱ��![]() ����Բ�ֱ�������
����Բ�ֱ�������![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г��ֱ�Ϊ1m��2m��3m�ĸֹܸ�3����ÿ���ֹ��ʵؾ��ȡ���ϸ��ͬ���в�ͬ�ı�ţ������������ȡ2����������ֹܱ���ȡ�Ŀ������Ǿ��ȵģ����ٽ���ȡ�ĸֹ���Ӻ��ɱ�ֱ��һ������X��ʾ�º��ɵĸֹܵij��ȣ��������ƣ���
��1����X�ķֲ��У�
��2����Y=����2X+��+1��E��Y����1����ʵ���˵�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����SnΪ����{an}��ǰn��ͣ���Sn=n2+n+1��n��N* ��
��1��������{an}��ͨ�ʽ��
��2��������{ ![]() }��ǰn���Tn ��
}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() (
(![]() Ϊ��Ȼ�����ĵ�������
Ϊ��Ȼ�����ĵ�������![]() .
.
��1��֤������![]() ʱ��
ʱ�� ![]() û����㣻
û����㣻
��2������![]() ʱ��
ʱ�� ![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ߴӵ㣨��2����3���������y�ᷴ�����Բ��x+3��2+��y��2��2=1���У������������ֱ�ߵ�б��Ϊ�� ��
A.�� ![]() ��
�� ![]()
B.�� ![]() ��
�� ![]()
C.�� ![]() ��
�� ![]()
D.�� ![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ�����Ϊ![]() �ĺ���
���![]() ���������
���������![]() ���ڵ�
���ڵ�![]() ����
����![]() ʱ������
ʱ������![]() ���۵�
���۵�![]() ����
����![]() ʱ��
ʱ�� ![]() �����
�����![]() Ϊ��ƫ�Գƺ��������ָ����ĸ�������
Ϊ��ƫ�Գƺ��������ָ����ĸ�������
��![]() �� ��
�� �� 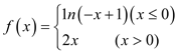 ��
��
��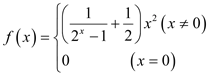 �� ��
�� ��![]() ��
��
����������ƫ�Գƺ������ĺ���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() ��.
��.
��1����![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ������
������![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2����![]() ������
������![]() �ϲ��ǵ�����������
�ϲ��ǵ�����������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com