
【题目】关于平面向量 ![]() ,
, ![]() ,
, ![]() ,下列结论正确的个数为( ) ①若
,下列结论正确的个数为( ) ①若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() ;
;
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,则k=﹣3;
,则k=﹣3;
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() 与
与 ![]() +
+ ![]() 的夹角为30°;
的夹角为30°;
④已知向量 ![]() ,且
,且 ![]() 与
与 ![]() 的夹角为锐角,则实数λ的取值范围是
的夹角为锐角,则实数λ的取值范围是 ![]() .
.
A.4个
B.3个
C.2个
D.1个
【答案】C
【解析】解:对于①,若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() (
( ![]() ﹣
﹣ ![]() )=0,不一定有
)=0,不一定有 ![]() =
= ![]() ,可能
,可能 ![]() ,(
,( ![]() ﹣
﹣ ![]() )垂直,故不正确; 对于②,若
)垂直,故不正确; 对于②,若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,即有﹣2k=6,则k=﹣3,故正确;
,即有﹣2k=6,则k=﹣3,故正确;
对于③,非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则|
|,则| ![]() |2=|
|2=| ![]() |2=|
|2=| ![]() ﹣
﹣ ![]() |2=|
|2=| ![]() |2+|
|2+| ![]() |2﹣2
|2﹣2 ![]()
![]() ,即有
,即有 ![]()
![]() =
= ![]() |
| ![]() |2 ,
|2 , ![]() (
( ![]() +
+ ![]() )=
)= ![]() 2+
2+ ![]()
![]() =
= ![]() |
| ![]() |2 , |
|2 , | ![]() +
+ ![]() |=
|= ![]() =
= ![]() |
| ![]() |,
|,![]() 与
与 ![]() +
+ ![]() 的夹角的余弦值为
的夹角的余弦值为  =
= ![]() ,由夹角的范围[0°,180°),可得夹角为30°,故正确;
,由夹角的范围[0°,180°),可得夹角为30°,故正确;
对于④,已知向量 ![]() ,且
,且 ![]() 与
与 ![]() 的夹角为锐角,
的夹角为锐角,
可得 ![]() (
( ![]() )>0,且
)>0,且 ![]() 与
与 ![]() 不共线,即有1+λ+2(2+λ)>0,且2(1+λ)≠2+λ,
不共线,即有1+λ+2(2+λ)>0,且2(1+λ)≠2+λ,
解得λ>﹣ ![]() 且λ≠0,故不正确.
且λ≠0,故不正确.
其中正确的个数为2.
故选:C.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,30名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编号为1﹣30号,再用系统抽样方法从中抽取6人,则其中成绩在区间[130,151]上的运动员人数是( ) 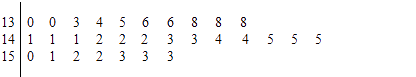
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和Sn , 且a3=7,S11=143, (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2 ![]() +2n,求数列{bn}的前n项和Tn .
+2n,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若△ABC的内角A,B,C的对边分别为a,b,c,已知c=2,C= ![]() .
.
(1)若b= ![]() ,求角B;
,求角B;
(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试中,五位学生的数学,物理成绩如下表所示:

(1)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;

(2)根据上表数据,画出散点图并用散点图说明物理成绩![]() 与数学成绩
与数学成绩![]() 之间线性相关关系的强弱,如果具有较强的线性相关关系,求
之间线性相关关系的强弱,如果具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:
回归直线的方程是![]() ,其中
,其中 ,
, ![]() ,
,
![]() 是与
是与![]() 对应的回归估计值,
对应的回归估计值,
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为2的线段A B两端点A和B分别在x轴和y轴上滑动,线段AB的中点M的轨迹为曲线C. (Ⅰ)求曲线C的方程;
(Ⅱ)点P(x,y)是曲线C上的动点,求3x﹣4y的取值范围;
(Ⅲ)已知定点Q(0, ![]() ),探究是否存在定点T(0,t)(t
),探究是否存在定点T(0,t)(t ![]() )和常数λ满足:对曲线C上任意一点S,都有|ST|=λ|SQ|成立?若存在,求出t和λ;若不存在,请说明理由.
)和常数λ满足:对曲线C上任意一点S,都有|ST|=λ|SQ|成立?若存在,求出t和λ;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{ an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(1)求数列{ an}的通项公式;
(2)若数列{bn}满足 ![]() +…+
+…+ ![]() =an (n∈N* ) 求数列{bn}的前n项和Sn .
=an (n∈N* ) 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程 ![]() =
= ![]() t+
t+ ![]() .
.
(Ⅱ)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
附:回归方程 ![]() =
= ![]() t+
t+ ![]() 中
中 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com