解:(1)K
AB=
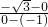
=-

,∴K
BC=

,
直线BC的方程是y+

=

x,,当y=0,得x=3,即点C(3,0),
所以,△ABC的外接圆M的圆心M(1,0),半径r=2.
圆M的方程是(x-1)
2+y
2=4;
(2)直线l的方程可化为y=
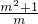
(x+1),令k=
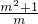
,
则l的方程为y=k(x+1),则直线l恒过圆M上的定点A(-1,0),
则直线l可能与圆相交.
因为|m|

(m
2+1),所以|k|=
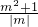
≥2,,当且仅当|m|=1时等号成立.
圆心M(1,0)到直线l的距离d=
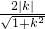
.(9分)
由|k|≥2,d=
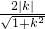
=
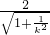
≥
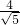
,即d>

.
从而圆M截直线l所得的弦所对的圆心角小于

.
所以直线l不能将圆M分割成弧长的比值为

的两段弧.(12分)
分析:(1)由A和B的坐标求出直线AB方程的斜率,根据两直线垂直时斜率的乘积为-1,由AB与BC垂直,求出直线BC的斜率,由B的坐标和求出的斜率写出直线BC的方程,令y=0求出x的值,确定出点C的坐标,求出斜边AC的长即为外接圆的直径,除以2可得圆的半径,利用中点坐标公式求出A和C的中点坐标即为外接圆的圆心M的坐标,由求出的圆心M的坐标和半径写出三角形ABC的外接圆M的方程即可;
(2)把直线l的方程变形可得直线l恒过点A(-1,0),而A在圆周上,故存在直线l可能与圆相交;由基本不等式求出|k|的最小值,利用点到直线的距离公式表示出圆心到直线l的距离d,根据|k|的最小值得出d的最小值,发现d的最小值大于半径的一半,从而圆M截直线l所得的弦所对的圆心角小于

,故直线l不能将圆M分割成弧长的比值为

的两段弧.
点评:此题考查了圆的标准方程,以及直线与圆的位置关系,涉及的知识有两直线垂直时斜率满足的关系,中点坐标公式,直线与坐标轴的交点,恒过定点的直线方程,点到直线的距离公式,以及基本不等式应用,直线与圆相交时,常常利用弦心距,弦的一半以及圆的半径构造直角三角形来解决问题.

 如图,直角三角形ABC的顶点坐标A(-1,0),直角顶点
如图,直角三角形ABC的顶点坐标A(-1,0),直角顶点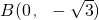 ,顶点C在x轴上.
,顶点C在x轴上.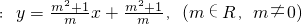 ,直线?能否与圆M相交?为什么?若能相交,直线?能否将圆M分割成弧长的比值为
,直线?能否与圆M相交?为什么?若能相交,直线?能否将圆M分割成弧长的比值为 的两段弧?为什么?
的两段弧?为什么?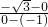 =-
=- ,∴KBC=
,∴KBC= ,
, =
= x,,当y=0,得x=3,即点C(3,0),
x,,当y=0,得x=3,即点C(3,0),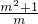 (x+1),令k=
(x+1),令k=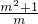 ,
, (m2+1),所以|k|=
(m2+1),所以|k|=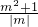 ≥2,,当且仅当|m|=1时等号成立.
≥2,,当且仅当|m|=1时等号成立.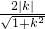 .(9分)
.(9分)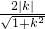 =
=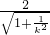 ≥
≥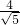 ,即d>
,即d> .
. .
. 的两段弧.(12分)
的两段弧.(12分) ,故直线l不能将圆M分割成弧长的比值为
,故直线l不能将圆M分割成弧长的比值为 的两段弧.
的两段弧.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=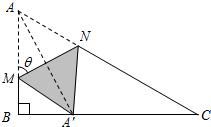 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC= (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答) (2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)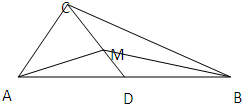 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.