
分析 利用特殊角的三角函数值,两角差的正弦函数公式,二倍角公式,诱导公式化简已知可得cosθ=3sinθ,利用同角三角函数基本关系式即可计算得解tanθ的值.
解答 解:∵$\sqrt{2}$sin($\frac{π}{4}$-θ)+2=4cos2($\frac{π}{4}$-$\frac{θ}{2}$),
∴$\sqrt{2}$($\frac{\sqrt{2}}{2}$cosθ-$\frac{\sqrt{2}}{2}$sinθ)+2=4×$\frac{1+cos(\frac{π}{2}-θ)}{2}$=2+2sinθ,整理可得:cosθ=3sinθ,
∴tanθ=$\frac{sinθ}{cosθ}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查了特殊角的三角函数值,两角差的正弦函数公式,二倍角公式,诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
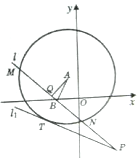 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
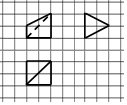 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | 12π | D. | $\frac{41}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com