
【题目】某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中,能较好地反映计算机在第![]() 天被感染的数量
天被感染的数量![]() 与
与![]() 之间的关系的是
之间的关系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π),其图象最低点的纵坐标是-![]() ,相邻的两个对称中心是(
,相邻的两个对称中心是(![]() ,0)和(
,0)和(![]() ,0).求:
,0).求:
(1)f(x)的解析式;
(2)f(x)的值域;
(3)f(x)图象的对称轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题中,正确的命题是:______.
(1)![]() 是奇函数,则
是奇函数,则![]() 的值为0;
的值为0;![]()
(2)若![]() ,则
,则![]() (
(![]() 、
、![]() 且
且![]() 、
、![]() );
);
(3)设集合![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 在
在![]() 单调递增,则
单调递增,则![]() 的取值集合为
的取值集合为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 和
和![]() ,若存在区间
,若存在区间![]() ,使
,使![]() 在区间
在区间![]() 上恒成立,则称区间
上恒成立,则称区间![]() 是函数
是函数![]() 和
和![]() 的“公共邻域”.设函数
的“公共邻域”.设函数![]() 的反函数为
的反函数为![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像关于点
的图像关于点![]() 对称.
对称.
(1)求函数![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求函数
,求函数![]() 的定义域;
的定义域;
(3)是否存在实数![]() ,使得区间
,使得区间![]() 是
是![]() 和
和![]() 的“公共邻域”,若存在,求出
的“公共邻域”,若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数f(x)的定义域,判断并证明函数f(x)的奇偶性;
(Ⅱ)是否存在这样的实数k,使f(k-x2)+f(2k-x4)≥0对一切![]() 恒成立,若存在,试求出k的取值集合;若不存在,请说明理由.
恒成立,若存在,试求出k的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形理论是当今世界十分风靡和活跃的新理论、新学科。其中,把部分与整体以某种方式相似的形体称为分形。分形是一种具有自相似特性的现象,图象或者物理过程。标准的自相似分形是数学上的抽象,迭代生成无限精细的结构。也就是说,在分形中,每一组成部分都在特征上和整体相似,只仅仅是变小了一些而已,谢尔宾斯基三角形就是一种典型的分形,是由波兰数学家谢尔宾斯基在1915年提出的,按照如下规律依次在一个黑色三角形内去掉小三角形则当![]() 时,该黑色三角形内共去掉( )个小三角形
时,该黑色三角形内共去掉( )个小三角形
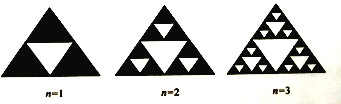
A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com