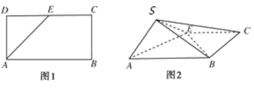
[题目]如图.点E为正方形ABCD边CD上异于点C.D的动点.将△ADE沿AE翻折成△SAE.使得平面SAE⊥平面ABCE.则下列说法中正确的有( )①存在点E使得直线SA⊥平面SBC,②平面SBC内存在直线与SA平行③平面ABCE内存在直线与平面SAE平行,④存在点E使得SE⊥BA．A．1个 B．2个 C．3个 D．4个题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列说法中正确的有（）

①存在点E使得直线SA⊥平面SBC；

②平面SBC内存在直线与SA平行

③平面ABCE内存在直线与平面SAE平行；

④存在点E使得SE⊥BA．

A．1个 B．2个 C．3个 D．4个

【答案】A

【解析】

试题分析：：①若直线SA⊥平面SBC，

则直线SA与平面SBC均垂直，则SA⊥BC，

又由AD∥BC，则SA⊥AD，这与∠SAD为锐角矛盾，故①错误；

②∵平面SBC∩直线SA=S，

故平面SBC内的直线与SA相交或异面，故②错误；

③取AB的中点F，则CF∥AE，由线面平行的判定定理，可得CF∥SAE平行，故③正确；

④若SE⊥BA，由EC∥AB，可得SE⊥EC，这与∠SEC为钝角矛盾，故④错误

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知二次函数的对称轴为，．

（1）求函数的最小值及取得最小值时的值；

（2）试确定的取值范围，使至少有一个实根；

（3）当时，，对任意有恒成立，求的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知四棱锥，底面为菱形，平面，，分别是的中点．

（Ⅰ）证明：；

（Ⅱ）若为上的动点，与平面所成最大角的正切值为，求二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】命题p：关于x的不等式x2＋2ax＋4＞0对于一切x∈R恒成立，命题q：x∈11,2]，x2－a≥0，若p∨q为真，p∧q为假，求实数a的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】市场上有一种新型的强力洗衣粉，特点是去污速度快，已知每投放（且）个单位的洗衣粉液在一定量水的洗衣机中，它在水中释放的浓度（克/升）随着时间（分钟）变化的函数关系式近似为，其中，若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和，根据经验，当水中洗衣液的浓度不低于4（克/升）时，它才能起有效去污的作用.