
【题目】已知等差数列![]() 满足
满足![]() ,前8项和
,前8项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() .
.
① 证明:![]() 为等比数列;
为等比数列;
② 求集合![]() .
.
【答案】(1)![]() (2)①见解析,②
(2)①见解析,②![]()
![]()
【解析】
(1)设等差数列{an}的公差为d.根据a4=4,前8项和S8=36.可得数列{an}的通项公式;
(2)①设数列{bn}前n项的和为Bn.根据bn=Bn﹣Bn﹣1,数列{bn}满足![]() .建立关系即可求解;
.建立关系即可求解;
②由![]() ,得
,得![]() ,即
,即![]() .记
.记![]() ,由①得,
,由①得,![]() ,
,
由![]() ,得cm=3cp>cp,所以m<p;设t=p﹣m(m,p,t∈N*),由
,得cm=3cp>cp,所以m<p;设t=p﹣m(m,p,t∈N*),由![]() ,得
,得![]() .讨论整数成立情况即可;
.讨论整数成立情况即可;
(1)设等差数列![]() 的公差为d.
的公差为d.
因为等差数列![]() 满足
满足![]() ,前8项和
,前8项和![]() ,
,
所以 ,解得
,解得![]()
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)①设数列![]() 前
前![]() 项的和为
项的和为![]() .
.
![]()
得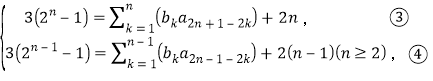
由③-④得
3![]()
-![]()
=![]()
-![]()
![]() .
.
所以![]()
![]() ,
,
又![]() ,所以
,所以![]() ,满足上式.
,满足上式.
所以![]()
当![]() 时,
时,![]()
由⑤-⑥得,![]() .
.
![]()
![]() ,
,
所以![]() ,
,![]() ,
,
所以数列![]() 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.
②由![]() ,得
,得![]() ,即
,即![]() .
.
记![]() ,由①得,
,由①得,![]() ,
,
所以![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立).
时等号成立).
由![]() ,得
,得![]() ,
,
所以![]() .
.
设![]()
![]() ,由
,由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,此时
,此时![]() 符合题意;
符合题意;
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,不合题意.
,不合题意.
下面证明当![]() 时,
时,![]() .
.
不妨设![]()
![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上单调增函数,
上单调增函数,
所以![]() ,
,
所以当![]() 时,
时,![]() ,不合题意.
,不合题意.
综上,所求集合![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-ABCD中,平面![]() 垂直于对角线AC,且平面
垂直于对角线AC,且平面![]() 截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
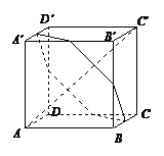
A. S为定值,l不为定值 B. S不为定值,l为定值
C. S与l均为定值 D. S与l均不为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支,简称为干支,源自中国远古时代对天象的观测.“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”称为十天干,“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”称为十二地支.干支纪年法是天干和地支依次按固定的顺序相互配合组成,以此往复,60年为一个轮回.现从农历2000年至2019年共20个年份中任取2个年份,则这2个年份的天干或地支相同的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |

其中![]() ,
,![]() .
.
为了预测印刷![]() 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷
的回归方程,并预测印刷![]() 千册时每册的成本费.
千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下面一道题目的证明,指出其中的一处错误。题目:平面上有六个点,任何三点都是三边互不相等三角形的顶点,则这些三角形中有一个的最短边又是另一个三角形的最长边。证明:第一步,对已知的六个点作两两连线,可以得出15条边,记为![]() ,
,![]() ,…,
,…,![]() .第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设
.第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设![]() .第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则
.第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则![]() 、
、![]() 、
、![]() 组成的三角形的最长边
组成的三角形的最长边![]() ,也是
,也是![]() 、
、![]() 、
、![]() 组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①若![]() 为真命题,则
为真命题,则![]() 为真命题;
为真命题;
②命题“![]() ,有
,有![]() ”的否定为“
”的否定为“![]() ,有
,有![]() ”;
”;
③“平面向量![]() 与
与![]() 的夹角为钝角”的充分不必要条件是“
的夹角为钝角”的充分不必要条件是“![]() ”;
”;
④在锐角三角形![]() 中,必有
中,必有![]() ;
;
⑤![]() 为等差数列,若
为等差数列,若![]() ,则
,则![]()
其中正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com